Discrete Mathematics Lesson 17: Relations
Upcoming
- Exam 2 posted today, due next Friday (4/21)
- Problem Presentations next week (4/17, 4/20).
- Problem Set 5: given 4/17, due 4/25 (Tuesday)
- Problem Set 6: given 4/24, due 5/1
- Lowest grade dropped
- Final Project (Presentation + Paper / Group)
- Choose a topic by 4/24
- Group Presentation in class on 5/1
- Paper due as a group 5/8
- Final Exam: given 5/1, due 5/8
Video
Watch the recording of the online lecture I gave in Fall 2020 on this topic. It’s about one hour. You can follow along with the notes below, or with the slides from that lecture.
You may also wish to consult the text An Infinite Descent into Pure Mathematics. Below we mostly cover chapter 5 on relations. Later we will look at section 11.1.
Relations
Definition: Let $X$ and $Y$ be sets. A binary relation $R$ from $X$ to $Y$ is a subset of $X \times Y$, that is, a set of ordered pairs $(x, y)$ where $x \in X$ and $y \in Y$.
- $X$ is the domain of $R$, $Y$ is the codomain
- If $X = Y$, we say $R$ is a “relation on $X$”
- Can think of it as a formula $R(x, y)$
- Write $x \mathrel{R} y$ for $(x, y) \in R$ or $R(x, y)$
Ordering
Classical example: $x, y \in \mathbb{Z}$, $R$ is $<$:
- $0 < 1$
- “How are the numbers 0 and 1 related? 0 is less than 1”
- Adds structure to $\mathbb{Z}$:
- Sets have no structure: just elements
- Relations add structure: how are elements related to each other?
Set vs Relation
Integers as a set vs integers as a relation:
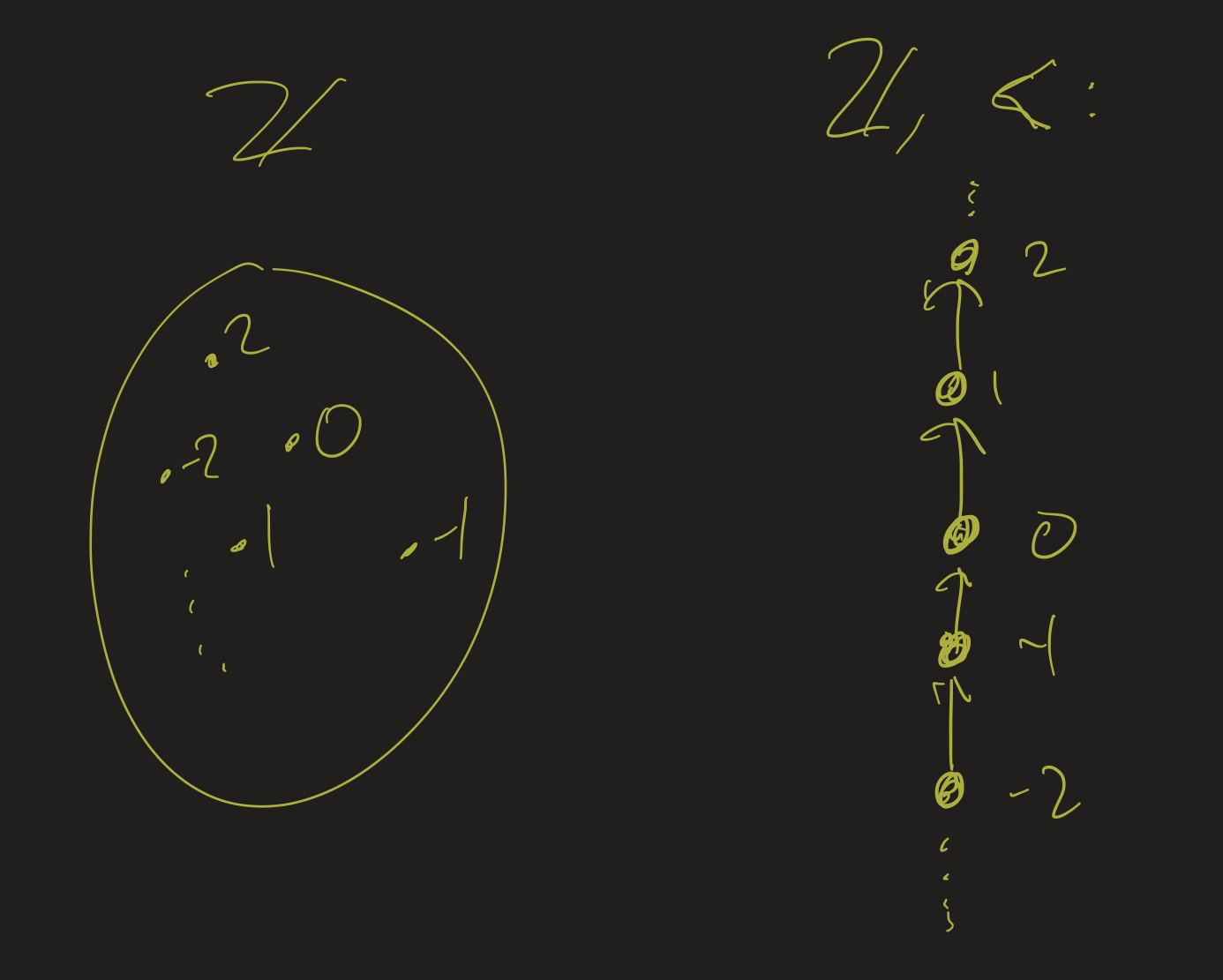
Two element relations:
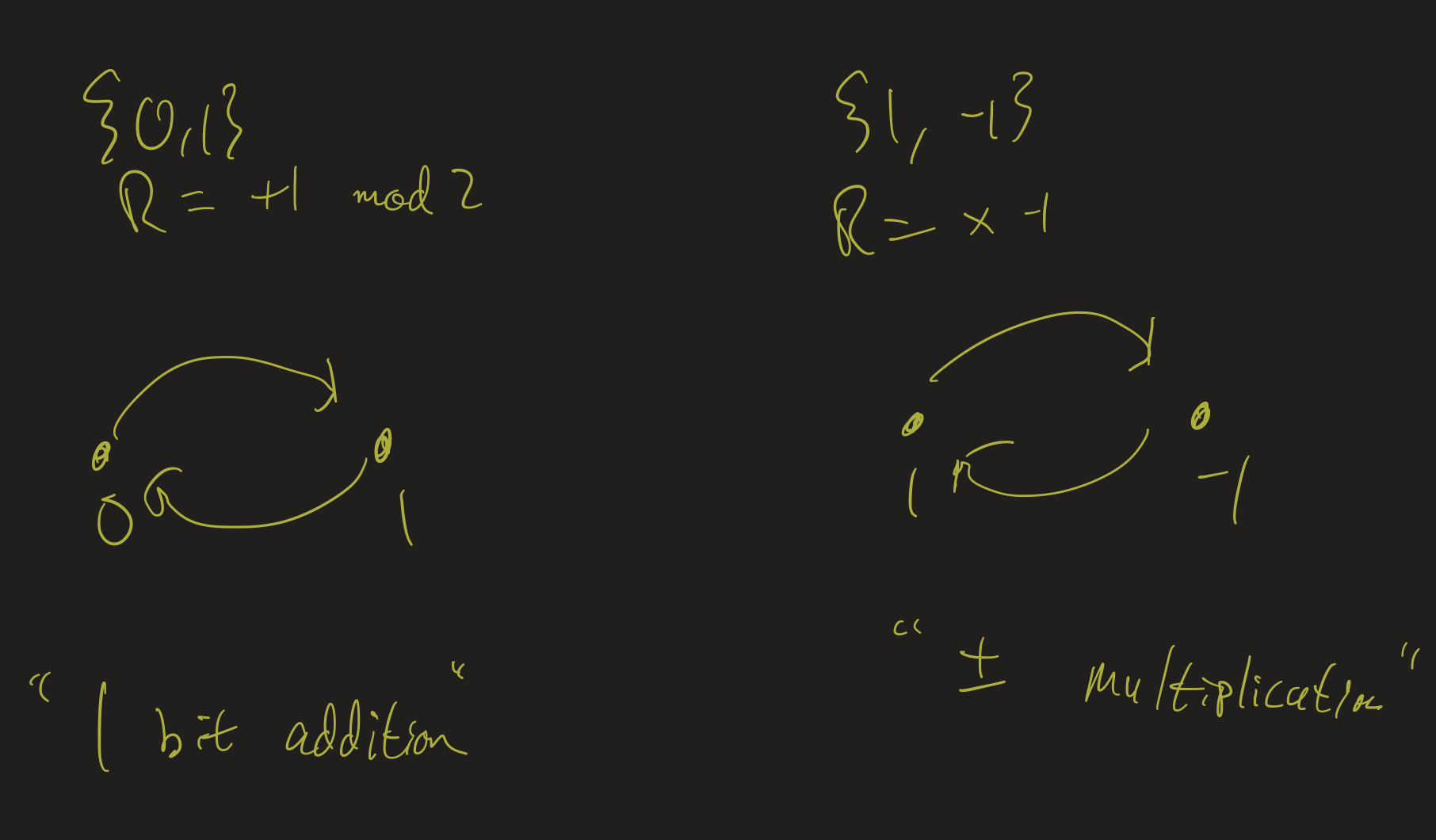
Rock, Paper, Scissors
Let $X = \{ $ rock, paper, scissors $ \} $. Let $x \mathrel{R} y$ mean “$x$ beats $y$ in a game of rock/paper/scissors”. Describe $R$ completely:
Solution
- rock beats scissors
- scissors beats paper
- paper beats rock
- So the set is: $\{$ (rock, scissors), (scissors, paper), (paper, rock) $\}$ and that's it.
Properties of Relations
- Reflexive: $\forall x (x \mathrel{R} x)$
- Symmetric: $\forall x \forall y (x \mathrel{R} y \rightarrow y \mathrel{R} x)$
- Transitive: $\forall x \forall y \forall z (x \mathrel{R} y \wedge y \mathrel{R} z \rightarrow x \mathrel{R} z)$
- Anti-symmetric: $\forall x \forall y (x \mathrel{R} y \wedge y \mathrel{R} x \rightarrow x = y)$
- Asymmetric: $\forall x \forall y (x \mathrel{R} y \rightarrow \lnot (y \mathrel{R} x))$
Examples: Reflexive
Let $X$ be the set of all people. Are the following relations reflexive: $\forall x (x \mathrel{R} x)$?
- “$x$ and $y$ are siblings.”
- “$x$ and $y$ share a parent.”
- “$x$ and $y$ are the same age.”
- “$x$ is older than $y$.”
- “$x$ is no younger than $y$”
Examples: Symmetric
Let $X$ be the set of all people. Are the following relations symmetric: $\forall x \forall y (x \mathrel{R} y \rightarrow y \mathrel{R} x)$?
- “$x$ and $y$ are siblings.”
- “$x$ and $y$ share a parent.”
- “$x$ and $y$ are the same age.”
- “$x$ is older than $y$.”
- “$x$ is no younger than $y$”
Examples: Transitive
Are the following relations transitive: $\forall x \forall y \forall z (x \mathrel{R} y \wedge y \mathrel{R} z \rightarrow x \mathrel{R} z)$?
- $X = \mathbb{Z}$, $R$ is: $x \leq y$.
- $X = \mathbb{Z}$, $R$ is: $x \mid y$
- $X = \{$ rock, paper, scissors $\}$, $R$ is “$x$ beats $y$”.
- $X$ is the collection of all finite subsets of $\mathbb{N}$, $R$ is “$\mid x \mid = \mid y \mid”.
Equivalence Relations
Let $X$ be a set. A relation $\sim$ on $X$ is called an equivalence relation if it is reflexive, symmetric, and transitive.
Definition
That is, $\sim$ is an equivalence relation on $X$ if:
- For all $x \in X$: $x \sim x$.
- For all $x, y \in X$, if $x \sim y$, then $y \sim x$.
- For all $x, y, z \in X$, if $x \sim y$ and $y \sim z$ then $x \sim z$.
The idea of an equivalence relation generalizes the following notions:
- $x = y$
- $x \equiv y$ (mod $n$) (Exam 2 Q2)
- Cardinality: $\mid A \mid$ = $\mid B \mid$
- Any notion of “sameness” (congruent shapes, similar triangles, etc)
Congruence modulo 3 is an equivalence relation:
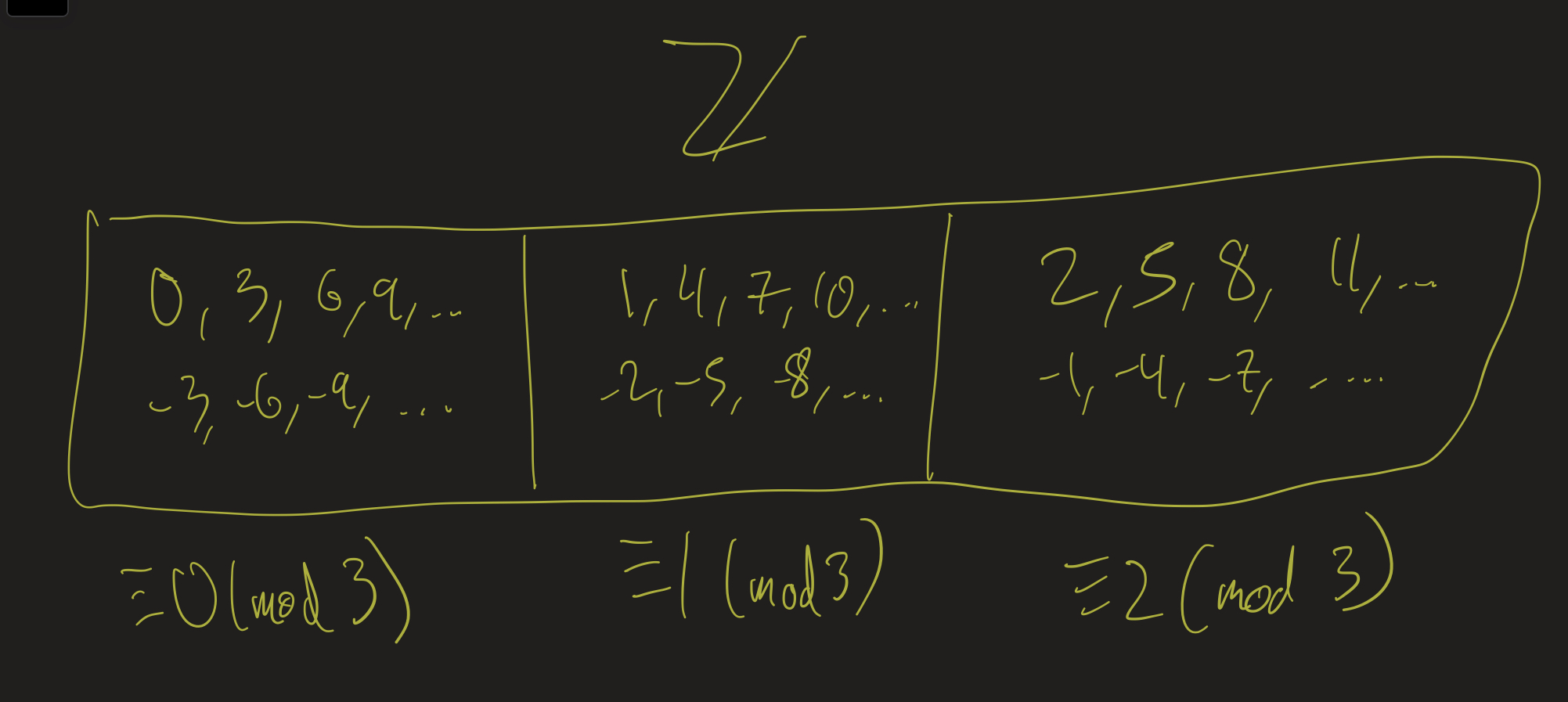
Equivalence Classes
- Generalizing the notion of “congruence classes”.
- Let $X$ be a set, $\sim$ an equivalence relation.
- Let $x \in X$. Then $[x]_{\sim} = { y \in X : x \sim y }$ is the equivalence class of $x$.
- The quotient of $X$ by ${\sim}$ is the set $X / {\sim} := \{ [x]_{\sim} : x \in X \}$.
- $x$ is called a representative of its equivalence class $[x]_{\sim}$.
- One equivalence class can have many representatives.
Examples
- $X = \mathbb{Z}$, $\sim$ is $\equiv$ (mod 2).
- Equivalence classes: evens and odds. $(X / {\sim}) = \{ E, O \}$.
- $X = \mathbb{Z}$, $\sim$ is $\equiv$ (mod 10).
- Equivalence classes?
- $x \equiv 0$ (mod 10) if its last digit is a 0.
- $x \equiv 1$ (mod 10) if its last digit is a 1.
- etc.
- In this case: \((X / \sim) = \{ [0]_{\sim}, [1]_{\sim}, \ldots, [9]_{\sim} \}.\)
Squares
Let $X = \mathbb{Z}$, and $x \sim y$ if $x^2 = y^2$. Claim: $\sim$ is an equivalence relation.
- Sketch a proof.
- What is the equivalence class of $0$? What is the equivalence class of $1$?
- How many equivalence classes are there?
- Find a good set of representatives.
Solution
- Proof: Each follows from reflexivity, symmetry, and transitivity of =
- $[0]_{\sim} = \{ 0 \}, [1]_{\sim} = \{1, -1 \}$
- One equivalence class for each non-negative number!
- Can represent using the elements of $\mathbb{N}$!
Sine
Let $X = \mathbb{R}$, and $x \sim y$ if $\sin(x) = \sin(y)$. Claim: $\sim$ is an equivalence relation.
- Sketch a proof.
- What is the equivalence class of $0$? What is the equivalence class of $\pi/2$?
- Find a good set of representatives.
Solution
- Proof: Again follows from reflexivity / symmetry / transitivity of =
- $[0]_{\sim} = \{0, \pi, 2\pi, -\pi, -2\pi, \ldots \} = \{ k\pi : k \in \mathbb{Z} \}$. For $\pi/2$: $[\pi/2]_{\sim} = \{ \pi/2 + 2\pi\cdot k : k \in \mathbb{Z} \}$.
- Before answering, look at the graph below:
Notice that every $y$-value on the graph of $y = \sin(x)$ appears in the interval from $x = -\pi/2$ to $x = \pi/2$. Therefore, a good set of representatives would be the interval $[-\pi/2, \pi/2]$.