Advising / Registration Spring 2021

• Calculus 1/2
• Computer Science I / II
• Data Structures
• Creating User Interfaces
• Drawing, Moving, and Seeing with Code (NME)

Spring semester starts February 1. No spring break.

Ordering

Classical example: \(x, y \in \mathbb{Z}\), \(R\) is \(<\):

• \(0 < 1\)
  • “How are the numbers 0 and 1 related? 0 is less than 1”
• Adds structure to \(\mathbb{Z}\):
• Sets have no structure: just elements
  • Relations add structure: how are elements related to each other?

Set vs Relation

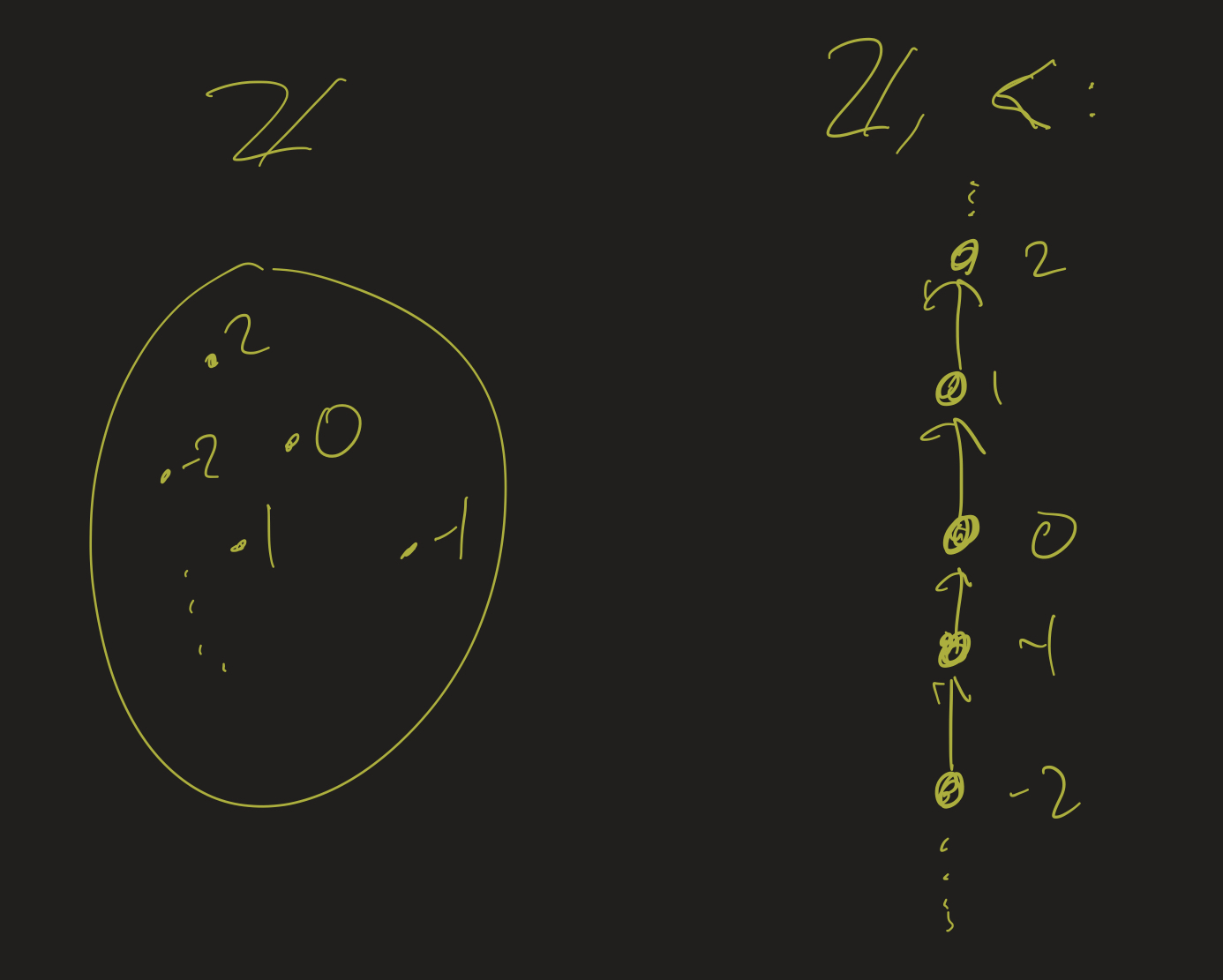
Rock, Paper, Scissors

Let \(X = \{\) rock, paper, scissors \(\}\). Let \(x \mathrel{R} y\) mean “\(x\) beats \(y\) in a game of rock/paper/scissors”. Describe \(R\) completely:

Properties of Relations

• Reflexive: \(\forall x (x \mathrel{R} x)\)
• Symmetric: \(\forall x \forall y (x \mathrel{R} y \rightarrow y \mathrel{R} x)\)
• Transitive: \(\forall x \forall y \forall z (x \mathrel{R} y \wedge y \mathrel{R} z \rightarrow x \mathrel{R} z)\)
• Anti-symmetric: \(\forall x \forall y (x \mathrel{R} y \wedge y \mathrel{R} x \rightarrow x = y)\)
• Asymmetric: \(\forall x \forall y (x \mathrel{R} y \rightarrow \lnot (y \mathrel{R} x))\)

Examples: Reflexive

Let \(X\) be the set of all people. Are the following relations reflexive: \(\forall x (x \mathrel{R} x)\)?

• “\(x\) and \(y\) are siblings.”
• “\(x\) and \(y\) share a parent.”
• “\(x\) and \(y\) are the same age.”
• “\(x\) is older than \(y\).”
• “\(x\) is no younger than \(y\)”

Examples: Symmetric

Let \(X\) be the set of all people. Are the following relations symmetric: \(\forall x \forall y (x \mathrel{R} y \rightarrow y \mathrel{R} x)\)?

• “\(x\) and \(y\) are siblings.”
• “\(x\) and \(y\) share a parent.”
• “\(x\) and \(y\) are the same age.”
• “\(x\) is older than \(y\).”
• “\(x\) is no younger than \(y\)”

Examples: Transitive

Are the following relations transitive: \(\forall x \forall y \forall z (x \mathrel{R} y \wedge y \mathrel{R} z \rightarrow x \mathrel{R} z)\)?

• \(X = \mathbb{Z}\), \(R\) is: \(x \leq y\).
• \(X = \mathbb{Z}\), \(R\) is: \(x \mid y\)
• \(X = \{\) rock, paper, scissors \(\}\), \(R\) is “\(x\) beats \(y\)”.
• \(X\) is the collection of all finite subsets of \(\mathbb{N}\), \(R\) is “\(|x| = |y|\)”.

Definition

That is, \(\sim\) is an equivalence relation on \(X\) if:

• For all \(x \in X\): \(x \sim x\).
• For all \(x, y \in X\), if \(x \sim y\), then \(y \sim x\).
• For all \(x, y, z \in X\), if \(x \sim y\) and \(y \sim z\) then \(x \sim z\).

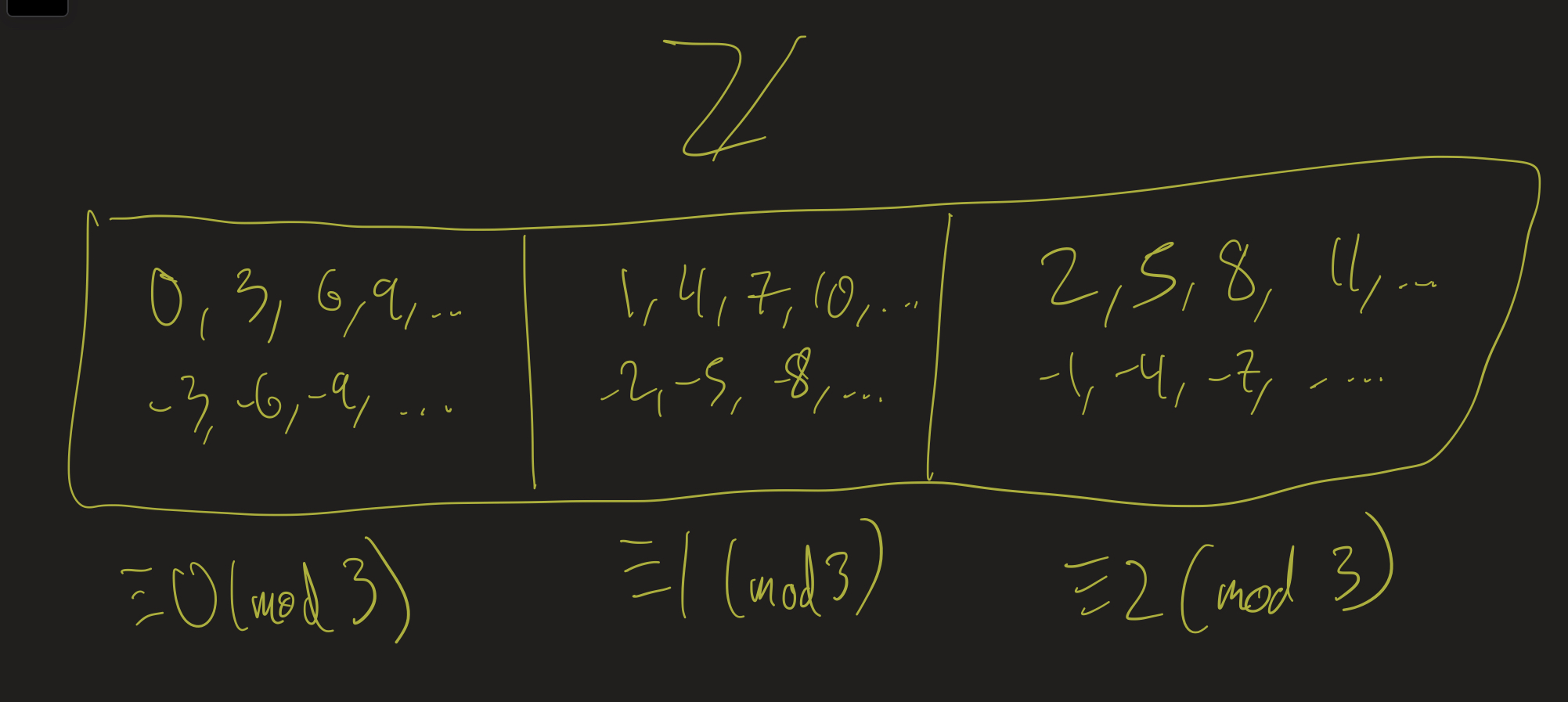
Equivalence Classes

• Generalizing the notion of “congruence classes”.
• Let \(X\) be a set, \(\sim\) an equivalence relation.
• Let \(x \in X\). Then \([x]_{\sim} = \{ y \in X : x \sim y \}\) is the equivalence class of \(x\).
• The quotient of \(X\) by \({\sim}\) is the set \(X / {\sim} = \{ [x]_{\sim} : x \in X \}\).
• \(x\) is called a representative of its equivalence class \([x]_{\sim}\).
  • One equivalence class can have many representatives.

Examples

• \(X = \mathbb{Z}\), \(\sim\) is \(\equiv\) (mod 2).
  • Equivalence classes: evens and odds. \(X / {\sim} = \{ E, O \}\).
• \(X = \mathbb{Z}\), \(\sim\) is \(\equiv\) (mod 10).
  • Equivalence classes?
  • \(x \equiv 0\) (mod 10) if its last digit is a 0.
  • \(x \equiv 1\) (mod 10) if its last digit is a 1.
  • etc.
  • \(X / {\sim} = \{ [0]_{\sim}, [1]_{\sim}, \ldots, [9]_{\sim} \}\)

Squares

Let \(X = \mathbb{Z}\), and \(x \sim y\) if \(x^2 = y^2\). Claim: \(\sim\) is an equivalence relation.

• Sketch a proof.
• What is the equivalence class of \(0\)? What is the equivalence class of \(1\)?
• How many equivalence classes are there?
• Find a good set of representatives.

Sine

Let \(X = \mathbb{R}\), and \(x \sim y\) if \(\sin(x) = \sin(y)\). Claim: \(\sim\) is an equivalence relation.

• Sketch a proof.
• What is the equivalence class of \(0\)? What is the equivalence class of \(\pi/2\)?
• Find a good set of representatives.

Squares / Check

• Proof: Each follows from reflexivity, symmetry, and transitivity of =
• \([0]_{\sim} = \{ 0 \}, [1]_{\sim} = \{1, -1 \}\)
• One equivalence class for each non-negative number!
• Can represent using the elements of \(\mathbb{N}\)!

Sine / Check

• Proof: Again follows from reflexivity / symmetry / transitivity of =
• \([0]_{\sim} = \{0, \pi, 2\pi, -\pi, -2\pi, \ldots \} = \{ k\pi : k \in \mathbb{Z} \}\).
• \([\pi/2]_{\sim} = \{ \pi/2 + 2\pi\cdot k : k \in \mathbb{Z} \}\).

Representatives?

Partitions

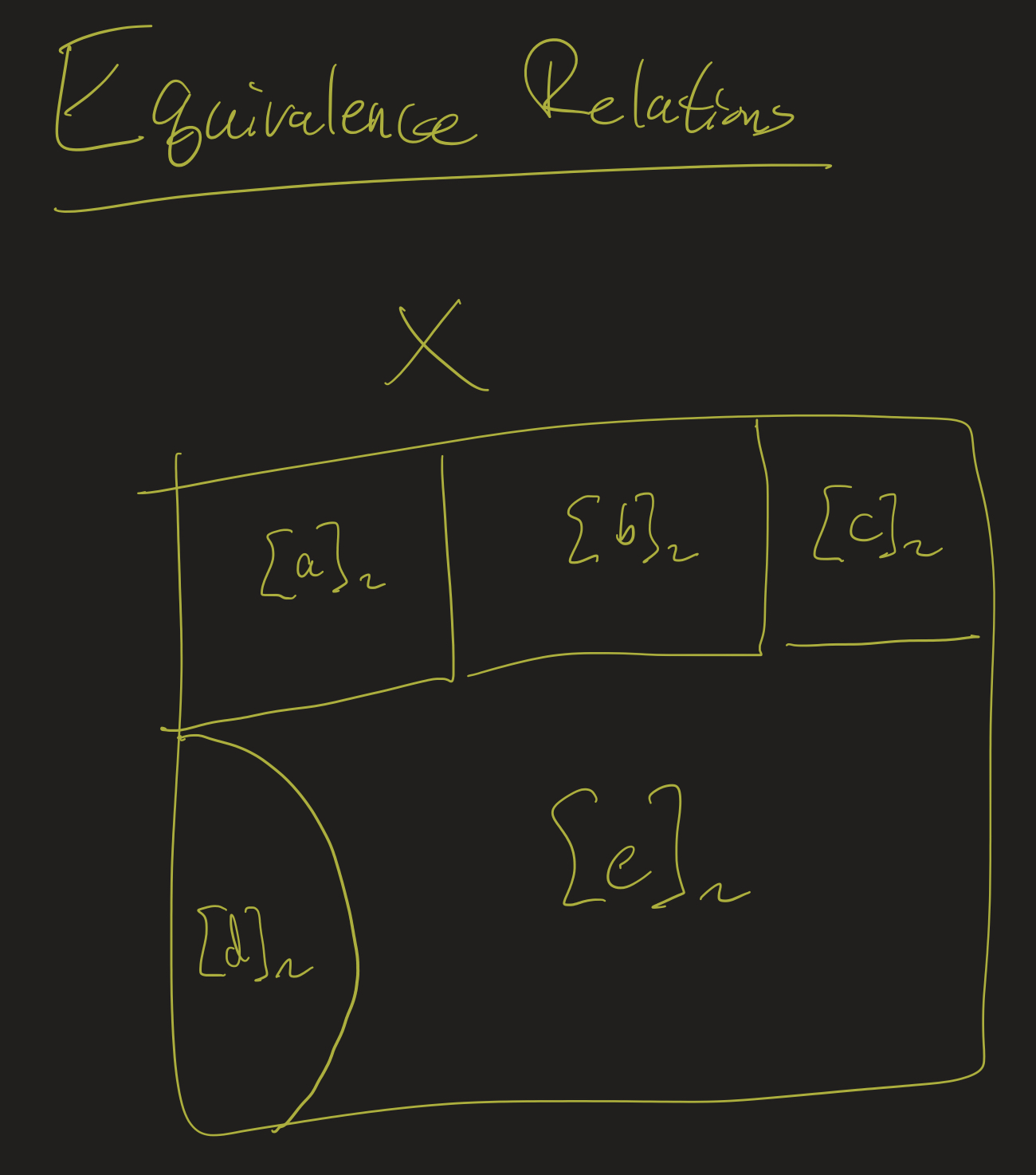
Partitions

• Claim: If \([x]_{\sim} \cap [y]_{\sim} \neq \emptyset\), then \([x]_{\sim} = [y]_{\sim}\).
• Proof? Problem set.
• Definition: Given a set \(X\), a partition of \(X\) is a of sets \(\{ X_i : i \in I \}\) is

Big Theta: Symmetric

• If \(f(n) = \Theta(g(n))\), then \(g(n) = \Theta(f(n))\)?
  • \(f = O(g)\) and \(g = O(f)\), so …
  • Not much to show here! Just given by definition.

Big Theta: Transitive

If \(f(n) = \Theta(g(n))\) and \(g(n) = \Theta(h(n))\), then \(f(n) = \Theta(h(n))\)?

• Show Big Oh is transitive first.
• There are \(N_1\), \(k_1\) such that \(f(n) \leq k_1 |g(n)|\) for all \(n \geq N_1\)
• There are \(N_2\), \(k_2\) such that \(g(n) \leq k_2 |h(n)|\) for all \(n \geq N_2\)
• Let \(N\) be the larger of \(N_1, N_2\). Then:
  • \(f(n) \leq k_1 g(n) \leq k_1 (k_2 |h(n)|)\) for all \(n \geq N\)
  • Let \(k = k_1 k_2\)

Big Theta: Transitive:

• If \(f = \Theta(g), g = \Theta(h)\):
• Then \(f = O(g), g = O(h)\), so by transitivity of O, \(f = O(h)\).
• \(h = O(g), g = O(f)\), so again by transitivity of O, \(h = O(f)\).
• Done!

Review of Definition

That is, \(\sqsubseteq\) is a partial order if:

• \(\forall x (x \sqsubseteq x)\)
• \(\forall x \forall y \forall z (x \sqsubseteq y \wedge y \sqsubseteq z \rightarrow x \sqsubseteq z)\)
• \(\forall x \forall y (x \sqsubseteq y \wedge y \sqsubseteq x \rightarrow x = y)\)

Divisibility (Maybe?)

• If \(X = \mathbb{Z}\), the relation \(\mid\) is not a partial order (why not?). But…
• If \(X = \mathbb{N}\), the relation \(\mid\) is a partial order (why?)

Generalizes:

• \(\leq\)
• \(\mid\) for \(\mathbb{N}\)
• \(\subseteq\) for sets
• Any notion of comparisons (but not Big Oh! Why not?)

Subsets

Let \(A\) be any set and \(X = \mathcal{P}(A)\). Then \(\subseteq\) is a partial order on \(X\).

• Reflexive: for all \(S \in X\), \(S \subseteq S\).
• Transitive: if \(S \subeseteq T\) and \(T \subseteq R\), then \(S \subseteq R\).
• Anti-symmetric: if \(S \subseteq T\) and \(T \subseteq S\), then \(S = T\).
  • This is how we prove set equality!