“Every” …

• “Every function \(f : A \to B\) is one to one.”
• This is a universal statement:
  • to prove it: let \(f : A \to B\) be a function. Show \(f\) must be one to one.
  • to disprove it: find a function \(f : A \to B\) that is not one to one.

Relations / Functions

Let \(A\) and \(B\) be sets and \(R \subseteq A \times B\). If, whenever \(x \in A\), there is exactly one \(y \in B\) such that \((x, y) \in R\), then \(R\) defines the graph of a one to one function. That is, there is \(f : A \to B\) such that \(R = \{ (x, f(x)) : x \in A \}\) and \(f\) is one to one.

Counterexample: \(A = \{ 0, 1 \}\), \(B = \{ a \}\), and \(R = \{ (0, a), (1, a) \}\).

• For each \(x \in A\):
  • \(x = 0\): how many \(y \in B\) are there such that \((x, y) \in R\)?
  • \(x = 1\): how many \(y \in B\) are there such that \((x, y) \in R\)?
  • “Whenever \(x \in A\), there is exactly one \(y \in B\)”?
• Is this function one to one?
  • \(x \neq y \rightarrow f(x) \neq f(y)\)?

Nesting Quantifiers

• \(\forall y \in B \exists x \in A (f(x) = y)\)

Consider \(A = \{ 0, 1 \}\), \(B = \{ a, b \}\). \(f(0) = a, f(1) = b\).

• As a question: for all \(y \in B\), is there \(x \in A\) such that \(f(x) = y\)?
  • If so: if I give you \(y\), can you tell me \(x\)?
  • \(y = a\)? What’s \(x\)?
  • \(y = b\)? What’s \(x\)?
  • True or False?

• \(\exists x \in A \forall y \in B (f(x) = y)\)

As before: \(A = \{ 0, 1 \}\), \(B = \{ a, b \}\). \(f(0) = a, f(1) = b\).

• Is there \(x \in A\) such that, for all \(y \in B\), \(f(x) = y\)?
  • If so: which \(x\)?
  • Is it \(x = 0\)?
  • Is it \(x = 1\)?
  • True or false?

Knights / Knaves (2(c))

• A: “If you asked B, they’d say C is a knight”
  • A is a knight if and only if “(B is a knight and C is a knight) or (B is a knave and C is a knave.)”
• B: A is a knave
  • B is a knight if and only if “A is a knave”
• C: A and I are the same type
  • C is a knight if and only if “(A is a knight and C is a knight) or”(A is a knave and C is a knave)."

• Case 1: A is a knight.
  • B and C are both knights, or both knaves.
  • If B is a knight, then A is a knave. Contradiction.
  • B is a knave, C is a knave? Consistent
• Case 2: A is a knave.
  • B is a knight and C is a knave? (C: “A and I are the same type” is true.)
  • B is a knave and C is a knight? (C: “A and I are the same type” is false.)
  • Impossible.

A is a knight, B is a knave, C is a knave.

“She say ‘Do you love me’…” (3(b))

I tell her “Only partly”
I only love my bed and my momma
I’m sorry

(Drake, “God’s Plan”)

• Among all possible objects of \(x\)’s affection, the only ones he loves are his bed and his momma
• For all \(y\), if \(x\) loves \(y\)…

Nesting Predicates?

• \(L(x, y)\) means “\(x\) loves \(y\)”
• \(M(x, y)\) means “\(x\) is the mother of \(y\)”
• \(L(x, M(x, y))\) means …?

Don’t Nest Predicates

• Inside a predicate: plug in objects (or variables)
• Predicates: represents a statement
• Moral of the story: don’t plug in a statement into a predicate. Combine using \(\wedge, \vee, \rightarrow\), etc.

• \(x\) loves his mother: “There is a person who is \(x\)’s mother and \(x\) loves this person.”
• \(x\) only loves his mother: \(x\) loves his mother (above) and for every \(y\), if \(x\) loves \(y\), then \(y\) is \(x\)’s mother.
• \(x\) only loves his bed and his momma: \(x\) loves his mother and \(x\) loves his bed and for every \(y\), if \(x\) loves \(y\), then either \(y\) is …

Nesting Quantifiers again (3(c))

• Read statements left-to-right.
• Starts with \(\forall x \ldots\): let \(x\) be an arbitrary member of the universe. Prove that … is true. (Or: find an example of \(x\) where “…” is false).
• Starts with \(\exists x \ldots\): find an example of \(x\) where “…” is true. Or: let \(x\) be an arbitrary member. Show “…” is false.

\(Y \setminus (Y \setminus X) = X\) (4(d))

• Set equality: \(A = B\) means “Every \(x \in A\) is in \(B\), and every \(x \in B\) is in \(A\).”
• Let \(x \in Y \setminus (Y \setminus X)\). Then … (definition of \(x \in Y \setminus (Y \setminus X)\)?)
• Let \(x \in X\). Then…

• Create slides (PPT, Google Slides, etc)
  • LaTeX? Beamer (if you’re interested)
• Describe the problem and outline the solution
• Keep it short: 5 minutes or so.
• Grading rubric will be posted (5% of grade)
• Presentation 2 will be in early April (4/3 - 4/13?).

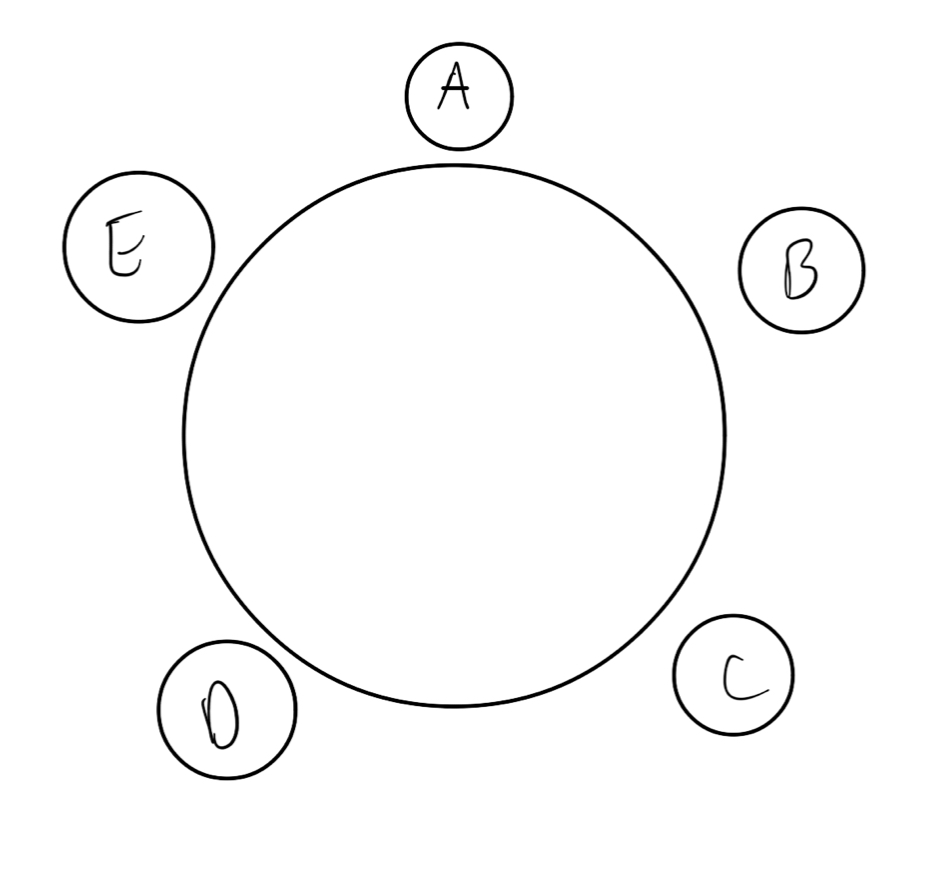
• 120 arrangements of 5 people.
• Cyclic arrangements? Depends on how you count:
  • 60? (if we care about orientation: clockwise / counterclockwise are different?)
  • 30 (if all we care about is “who is sitting next to whom”)

Other “counting” problems:

• Married couples must sit together
• Persons x and y don’t like each other
• etc.

Ex: Powers of 2

• 1 = 1
• 1 + 2 = 3
• 1 + 2 + 4 = 7
• 1 + 2 + 4 + 8 = 15
• 1 + 2 + 4 + 8 + 16 = 31

Hmmm

• 1 = 2 - 1
• 3 = 4 - 1
• 7 = 8 - 1
• 15 = 16 - 1
• 31 = 32 - 1

Aha!

Conjecture: The sum of the powers of \(2\) from \(2^0\) to \(2^{n}\) is \(2^{n+1} - 1\).

Can we prove this by induction?

\[P(n): \sum_{i=0}^{n} 2^i = 2^{n+1} - 1\]

Base case: \(P(0): 2^0 = 2^1 - 1\) is true.

Inductive Step

Let \(n \in \mathbb{N}\) (arbitrary natural number). Suppose \(P(n)\) is true. This means:

\[\sum_{i = 0}^n 2^i = 2^{n+1} - 1\]

We want to show that \(P(n+1)\) is also true.

How can we use what we know about \(\sum\limits_{i=0}^n 2^i\) to help us figure out \(\sum\limits_{i=0}^{n+1} 2^i\)?

Division and Remainder

Theorem: Let \(n \in \mathbb{Z}\) and \(k > 0\). There are unique \(q, r \in \mathbb{Z}\) such that \(n = qk + r\) and \(0 \leq r < k\).

Proof? (Actually non-trivial, but we will omit it.)

Symmetry

Theorem: Let \(n \in \mathbb{N}\), \(n > 0\), and \(x, y \in \mathbb{Z}\). If \(x \equiv y\) (mod \(n\)), then \(y \equiv x\) (mod \(n\)).

What needs to be proved here? What do we assume?

Reflexivity

Theorem: Let \(n \in \mathbb{N}\), \(n > 0\), and \(x \in \mathbb{Z}\). Then \(x \equiv x\) (mod \(n\)).

Again: what needs to be proved here? What do we assume?

Transitivity

Theorem: Let \(n \in \mathbb{N}\), \(n > 0\), and \(x, y, z \in \mathbb{Z}\). If \(x \equiv y\) (mod \(n\)) and \(y \equiv z\) (mod \(n\)), then \(x \equiv z\) (mod \(n\)).

Proof (idea): Let \(n \in \mathbb{N}\), \(n > 0\), and \(x, y, z \in \mathbb{Z}\). Suppose \(n\) divides \(x - y\) and \(n\) divides \(y - z\). Then…?

(Show \(n\) divides \(x - z\). How? Write down, explicitly, the definitions of “\(n\) divides \(x - y\)” and “\(n\) divides \(y - z\)”. Then manipulate things to show that the definition of \(n\) divides \(x - z\) is also satisfied.)