Additional Context

Each integer requires 4 bytes of space. Can we store them all in memory? If not, how do we sort them if we can’t store all at once?

Discuss. Design your best solution. (5-10 minutes.)

Induction

To prove a statement for every number \(n\):

1. Prove that the statement is true when \(n = 0\). (Base case)
2. Prove that, for any natural number \(k\), if the statement is true when \(n = k\) (fixed), then the statement still holds for \(n = k + 1\). (Inductive step)

Base case: h = 0

• Prove that there are \(2^{1} - 1\) nodes in a complete binary tree of height \(0\), assuming the last level is completely filled.
• What is a tree of height 0?

Inductive step

• Suppose we know that, for some arbitrary \(h\), there are \(2^{h+1} - 1\) nodes in a complete binary tree of height \(h\), assuming the last level is completely filled.
• Consider a complete binary tree of height \(h + 1\). What does that look like?
  • Has a root, which has two subtrees… of height?
  • (Using inductive assumption) How many nodes in those subtrees?
  • Therefore: how many nodes total?
• Conclusion: this tree has \(2^{h+2} - 1\) nodes.

Set operations

For our perspective, we consider the following operations on a set:

• contains
• insert
• remove
• size

Sometimes “insert” / “remove” are boolean methods, to indicate whether you were able to successfully modify the set (returning false, for example, if you tried to insert a duplicate).

Possible implementations

• ArrayList? Already has these operations. Running times? Can you get \(O(1)\) insert if you don’t allow duplicates?
• Tree?
  • Generic type must implement Comparable
  • Trees have contains / insert / remove.
  • We can impelment a “size” easily, just keep track of it whenever we call insert or remove.
  • Our implementation didn’t allow duplicates.
  • Running times?

ArrayList implementation

Exercise: Using an ArrayList, implement the Set interface. Analyze the time complexity of contains / insert / remove.

Starter code?

Better Implementation?

• All we care about: is \(x\) in the set or not?
• Do we need to store elements in order?
• Focus on integers:
  • Trade-off: use a huge amount of space.
  • Can we make insert / remove / contains \(O(1)\)?

Operating?

• Add a data item to the set?
  • Compute \(f(item)\), insert item into table[f(item)]
• Check if item is in the set? Check table[f(item)] == null
• Remove?

Hashtables

• This is the idea behind a hashtable.
• Lots of analysis needs to be done
  • How do we define a good hash function?
  • What is the likelihood of a collision?
  • What happens if there are collisions?

Video

Example

• Example (integer keys): \(h(x) = x\) mod \(s\).
• In what scenarios would this be a good hash function?
• Bad?
• Choose a good table size \(s\) to avoid these problems?

String Keys

Simple idea: think of a word as a number in base 27 (“a” represents the digit 1, and “z” represents the digit 27), then convert it to an integer.

• “abc” hashes to \(27^2 \times 1 + 27 \times 2 + 3\).
• What do we do if this value ends up larger than the hashtable size?
• Any major problem with this approach? (Hint: what characters can make up a String?)

Let’s look at the built-in hash function for Strings in Java.

Video

Probability

Insert \(N\) items into a table of size \(s\). Suppose the hash function is uniform. What’s the probability of a collision?

• \(N = 2, s = 4\)?
  • Two elements: \(x\) and \(y\).
  • Probability that \(h(x) == h(y)\)?
  • Probability that \(h(x) \neq h(y)\) is 3/4, so probabiliyt of collision is \(1/4\).

N = 3, s = 9

• Three: \(x, y, z\). Probability that \(h(x) == h(y)\) or \(h(x) == h(z)\) or \(h(y) == h(z)\)?
• Maybe easier to solve: probability that \(h(x)\), \(h(y)\) and \(h(z)\) are all different!
• Probability of a collision then is \(1 - Prob(h(x), h(y), h(z)\) are different\()\).

N = 4, s = 9

• Same idea, first find the probability that all four hash values are different
• Then subtract from 1.

Birthday Problem

• \(N = 23\), \(s = 365\) is the famous birthday problem!
• In a room with 23 people, there is a greater than 50% chance that two of them have the same birthday!
• What does this have to do with hash collisions?
  • What’s the “hash function” here?
  • What are the “keys” here?
• In general, if \(N > \sqrt{s}\), there is a good chance of a collision.

Video

Think about

As we learn about these, keep this question in mind: in what scenarios (in terms of the table size \(s\) and the number of insertions \(N\)) might we prefer one scheme over the other?

Load Factor

• Let \(N\) be number of elements to insert into the table.
• Let \(s\) be the size of the table.
• \(\lambda = \dfrac{N}{s}\) is called the load factor of the table.
• \(\lambda\) small: few collisions, lots of wasted space
• \(\lambda\) large: space used efficiently, but high chance of collisions.

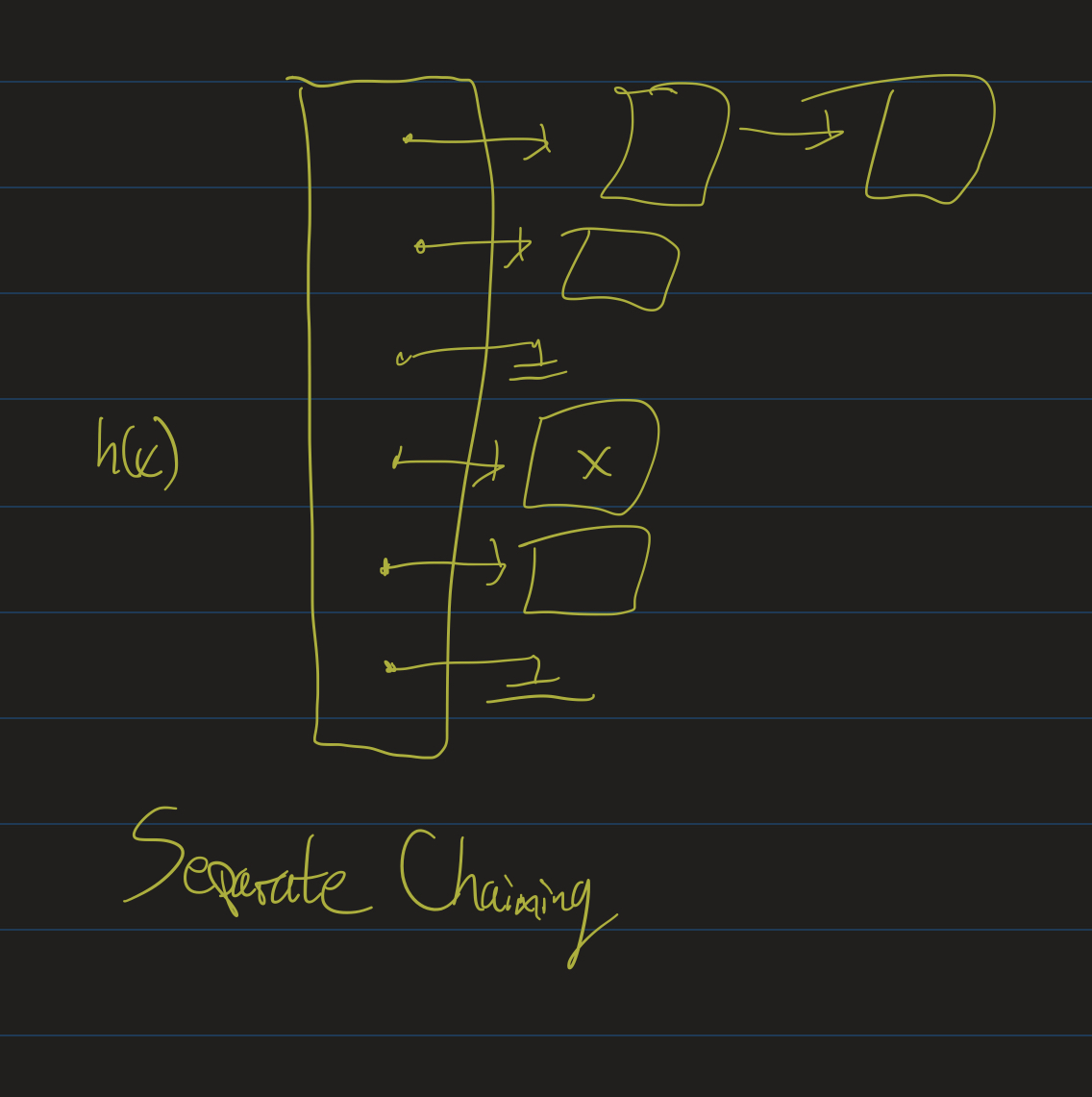
Separate Chaining

• Don’t keep a “large array”.
• Instead: keep an array of \(s\) lists.
• Think of each list as a “bucket” (or “bin”).
• Elements that hash to the same value go in to the same bucket.

Image

Running times

• Insert \(x\): compute hashcode \(h(x)\), add \(x\) to the \(h(x)\)-th list.
• Running time of insert?
• contains: compute the hash function, check the relevant list.
• Running time (average case)? Worst case?
• What happens as \(\lambda\) increases?
• Can we keep a bound on \(\lambda\)?

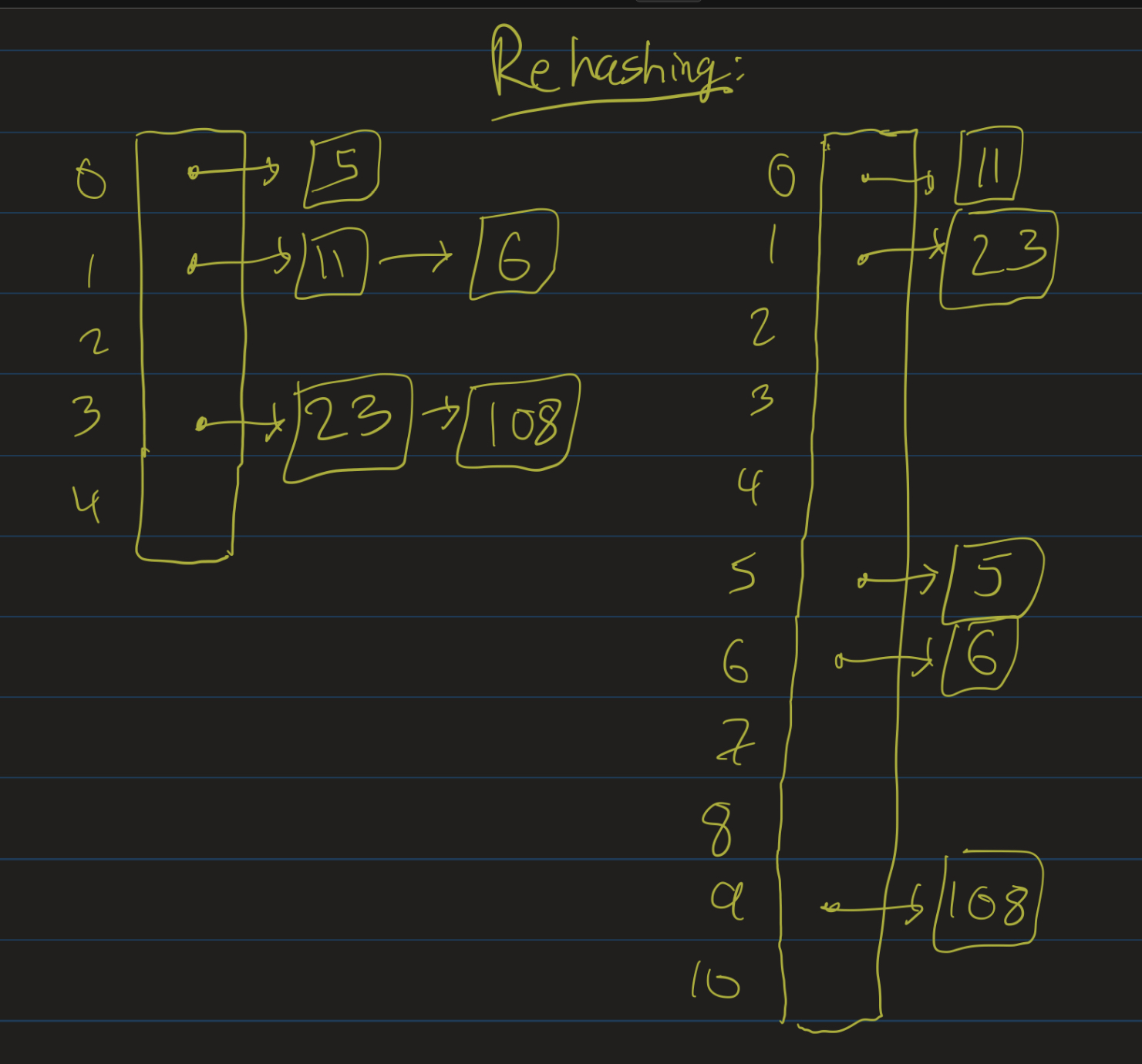
Rehashing

• If we allow \(\lambda\) to increase without bound, performance degrades.
• Many implementations (including Java’s) will rehash if it increases too much.
• Increase the size of the table (usually: pick the next prime number \(p > 2s\)).
• Go through each previously inserted item, and re-insert into the new table.
• Should not happen too often, so that we still get (amortized) constant time inserts.

Image

Video