Data Structures
Professor Abdul-Quader
Lesson 6 (Trees / Rotations)
Presentations
Start with problem presentations.
Project
Project hints / questions?
Postfix Calc
- Parse the text file
- For each line, instantiate a new stack (of integers).
- While parsing a line, if you see a number, push.
- If you see an operation, pop two numbers from the stack.
- if-then or switch-case to figure out what to push back on
- Fancier: enum types.
- When done with the line, pop the stack and output.
Base counter
- Queue of Strings.
- Enqueue all digits from 1 to \(base - 1\) as Strings.
- Repeat \(num\) times:
- Dequeue a “number” (as a String)
- Print it out.
- For each “digit” from 0 to \(base - 1\), enqueue “number” + “digit”
BinaryTree
Today:
- contains / remove
- some mathematics / theory / running times
- rotations
- balancing
Contains
Binary search:
- If item < root, check root.left (recursion)
- If item > root, check root.right (recursively)
- If item == root, return true.
- When do we return false? Base case?
Code
Remove
- Method signature should be void, not
boolean - if the node is a leaf, return null
- if the node has one child, replace its data with its child, delete its child.
- if the node has two children, replace its data with its successor, delete the successor
One Child
Successor
Remove
Running times
- BinaryTree of integers.
- Suppose \(N\) integers are inserted randomly.
- Running time of insert? Contains? Remove?
- What if insertion is not so random? Worst case?
Theory
- The level of a node in a tree is the length of the path from the root to that node. Example: the root is at level \(0\), its children are at level \(1\), etc. The height of the tree is equal to the highest level of the tree.
- A full binary tree is a tree for which every non-leaf node has exactly 2 children.
- A complete binary tree is a binary tree in which every level (possibly except the last) is completely filled, and all nodes are as fall left as possible.
Theorem
Exercise (Might be homework at some point): Suppose \(T\) is a complete binary tree of height \(h\) and the last level is completely filled. Then \(T\) has exactly \(2^{h+1} - 1\) nodes.
Therefore: a complete binary tree of height \(h\) has between \(2^h\) and \(2^{h+1} - 1\) nodes. That is:
- a tree of height 0 will have 1 node
- a tree of height 1 will have between 2 and 3 nodes
- a tree of height 2 will have between 4 and 7 nodes
- a tree of height 3 will have between 8 and 15 nodes
Height
- If \(T\) is a complete tree with \(N\) nodes, then its height is \(\lfloor \log_2(N) \rfloor\); that is, the height of the tree is \(O(\log(N))\).
- Insert: \(O(\log(N))\) steps in this case then (need to travel down one path of a tree from the root to a leaf, then insert below that leaf)
- That is, insertion doesn’t happen until the “subtree” is null. That takes \(h\) steps, where \(h\) is the height of the tree.
- Contains? On average, how many steps will it take to find a node in the tree?
Contains
- For each node at level \(l\), it takes \(l\) steps to find that node.
- \(2^l\) nodes on each level (you can prove this by induction), and \(2^{h+1} - 1\) nodes in total
- Average level of a node is \(\dfrac{1}{2^{h+1} - 1} \sum_{l=1}^{h} l \times 2^l\).
- Sum? Hard. Just find an upper bound.
- Since \(l \leq h\), above is \(\leq \dfrac{h}{2^{h+1} - 1} \sum_{l=1}^h 2^l\)
- Sum of \(2^l\) from \(l = 1\) to \(h\) is \(2^{h+1} - 2\), this is roughly \(h\), or \(O(\log(N))\).
Worst Case
Remember, the running times are all based on the height of the tree. Given a tree with \(N\) nodes, what’s the worst possible height of such a tree? What insertion order gives that height?
Preventing
Next topic: trees that are self-balancing, which will prevent the tree from getting too unbalanced.
Tree Rotations
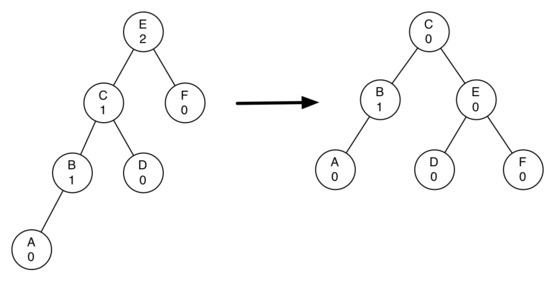
- Preserves “Search Tree” property
- Algorithm?
Right Rotation
L = root.left
root.left = L.right
L.right = root
return LMakes L the new root of this subtree.
Left Rotation
Similar idea:
R = root.right
root.right = R.left
R.left = root
return R- Makes R the new root of this subtree
- Inverse operations:
- Right rotation followed by left rotation?
Balancing
What does an “unbalanced” tree look like?
Unbalanced Trees
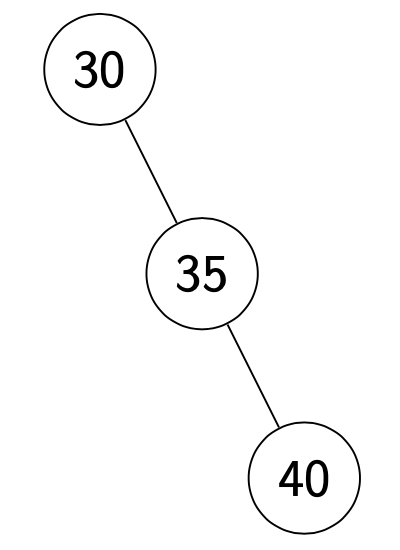
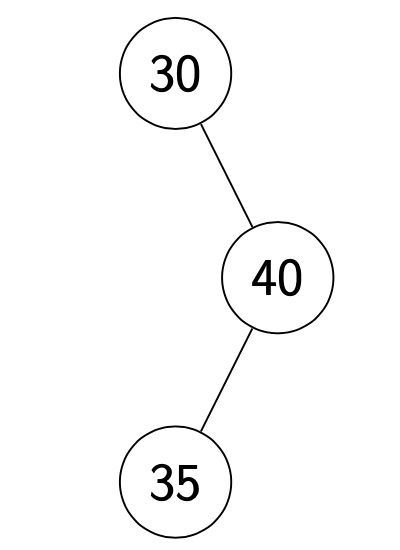
Unbalanced Trees
- Can also define left-right and left-left unbalanced trees
- In general:
- if heights of left and right subtrees differ by more than 1
- Keep track of the height of each node
- If one subtree has a larger height than the other, rebalance
- How do we rebalance? Tree rotations!
Algorithms for balancing
Some unbalanced trees can be rebalanced easily:
- right-right: rotate left
- left-left: rotate right
Right-left

- Rotate left around 30?
- Rotate right around 30? (can’t!)
- Solution?
Exercise
Forget about the code for a bit. What should a self-balancing tree do when we insert in the following order: 1, 2, 3, 4, 5, 6, 7?
Draw the pictures of the BSTs that result. When do we trigger a “rebalancing”?