Deadlines

• HW 4: Friday, 4/25
• Presentation 3 (online): Monday, 4/28

Exercise

Consider an \(n\) by \(n\) matrix \(M\), whose rows and columns are each sorted in increasing order. That is, the elements of each row increase as you go left to right, and the elements of each column increase as you go down. Determine if a number \(x\) is in the matrix in \(O(n)\) comparisons.

Greedy Algorithms

Greedy algorithm: attempts to find a solution to a problem by making choices that are locally optimal.

Hope: you find the globally optimal solution.

Often times: the greedy solution is not always globally optimal (in fact, it can sometimes produce the worst possible output).

Example

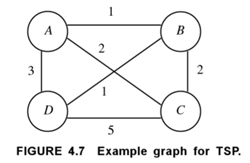
(Basu, Design Methods and Analysis of Algorithms). Greedy solution starting at \(A\)? Correct solution starting at \(A\)?

Change Making

(General) Problem: given a set of coin denominations \(\{ c_1 > c_2 > \ldots > c_n \}\), and a value \(x\), find the least number of coins needed to add up to \(x\).

Claim: standard coin denominations: \(\{ 1, 5, 10, 25 \}\): greedy algorithm produces an optimal colleciton of coins. (Proof is not hard, but is not very interesting. Look at all the cases for everything below \(24\).)

Exercise: show what the greedy algorithm outputs with this set of denominations and \(x = 37\). Then we will describe the algorithm generally.

Greedy Failure

The greedy algorithm fails for more general sets of coin denominations! Can you find a counterexample where the set of denominations is \(\{ 1, 15, 20 \}\)?

Video

Project 3

• Can either implement the greedy coloring algorithm or look up another coloring algorithm.
  • Running time of greedy coloring?
  • Why doesn’t it solve P = NP?
• Many other ideas can be found online.
  • Might find one that outputs a minimal coloring!
  • Why wouldn’t it solve P = NP? (Analyze its running time!)
• Don’t forget about the write-up (explain all of the above / try to break your algorithm if possible.)

Quick check

• Insertion sort: is this an online or an offline algorithm?
• Selection sort: is this an online or an offline algorithm?

Secretary Problem

Given a list of candidates for a job opening, you wish to hire the best one.

• Offline version: interview each one. After all interviews, call the best candidate.
• Online version: candidates all expect a decision right away. Once you hire someone, you can no longer interview the rest of the candidates. Once you reject someone, you can no longer get back to them.

(Sometimes referred to as the “Marriage” problem.)

Exercise

Discuss a potential hiring strategy. Suppose that there are 10 candidates and you can unambiguously rank them (if you were able to see them all). What strategy will optimize the probability that you hire the best candidate?

Video

Processes

• Process: a program in execution.
  • What does the CPU need to keep track of when a program is running?
  • What if there are multiple instances of the same program running?
• Example: IntelliJ, 37 different Chrome tabs, Outlook, etc all running on my computer at the same time.
  • But… how????

Threads

• Thread: a lightweight process.
• We still have the same program running, but different parts of the program could be executing at the same time.
• Same heap memory is allocated for everything.
• Each thread has its own:
  • Stack memory (local memory)
  • Program counter (line of code that the thread is sitting on)

Thread object

• java.util.Thread object (JVM Thread)
• When the JVM thread is created, the JVM allocates stack memory, creates the program counter, and asks the OS to create an OS thread.

Context switching

• Too many threads running: time-slicing.
• OS schedules each thread to run for short “slices” of CPU clock
• Then pause a thread and then run another thraed.
• Threads are paused / unpaused somewhat randomly.
• Context-switching: when the OS switches from one thread to another.
  • The context is the state of the thread (Prog Counter / stack memory).

Race Condition

• Why does this program not work?
• There is a race condition
  • When the behavior of a program depends on which instructions go first.
• What’s the race condition?

Incrementing

++counter;

Not just one instruction! Actually:

temp = counter;
temp2 = temp + 1;
counter = temp2;

Video

Reminders

• Final Groups?
  • Let me know by this weekend.
  • Everyone else will be assigned a group randomly.
• Project 3 due Monday.
• HW 4 due Friday.
• Presentation 3 due the following Monday.