Breaking the algorithm?

• Most end up using the greedy coloring algorithm.
• How might this fail to produce the fewest colors?
• Vertex Order!

Example 1

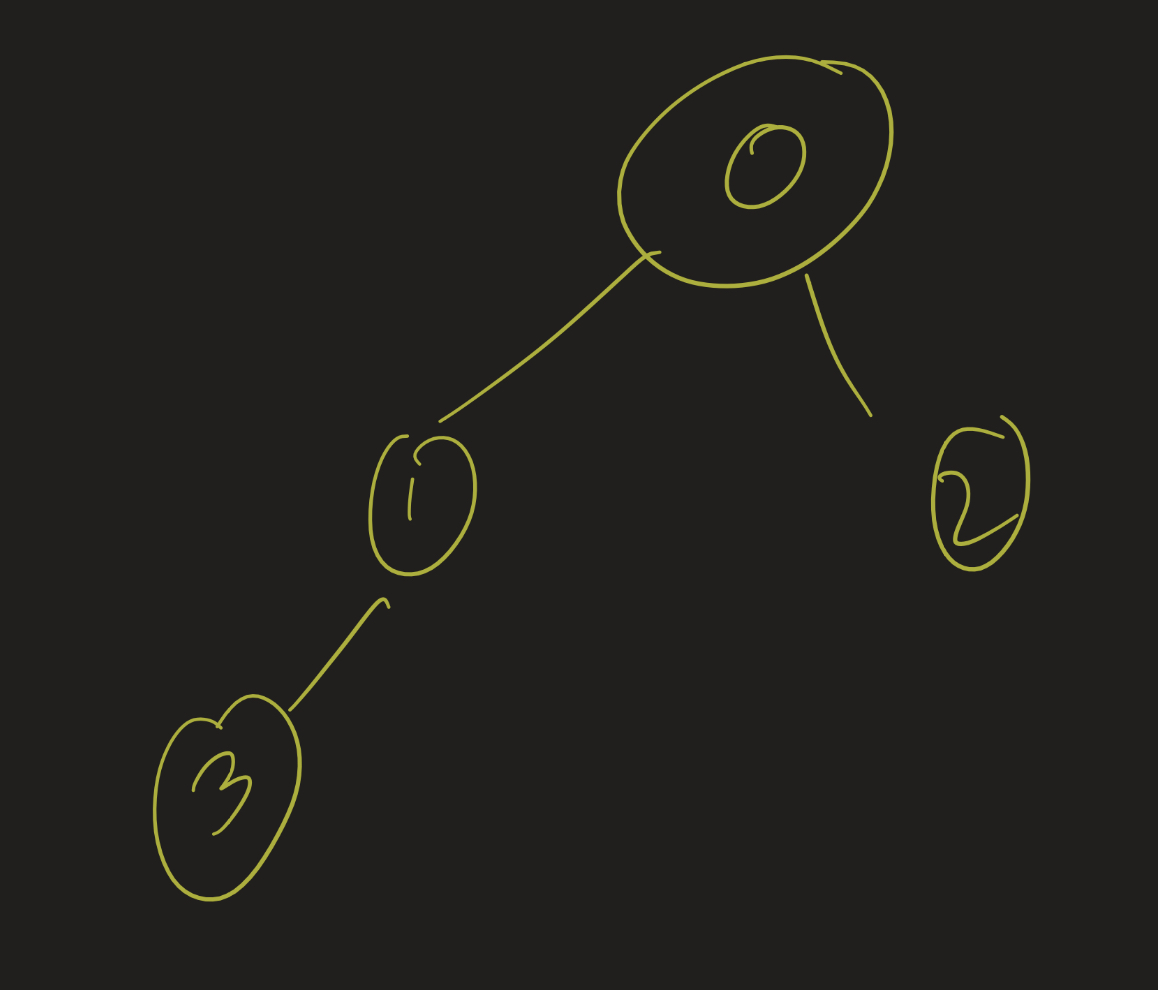
Color vertices in order. How many colors?

Example 2

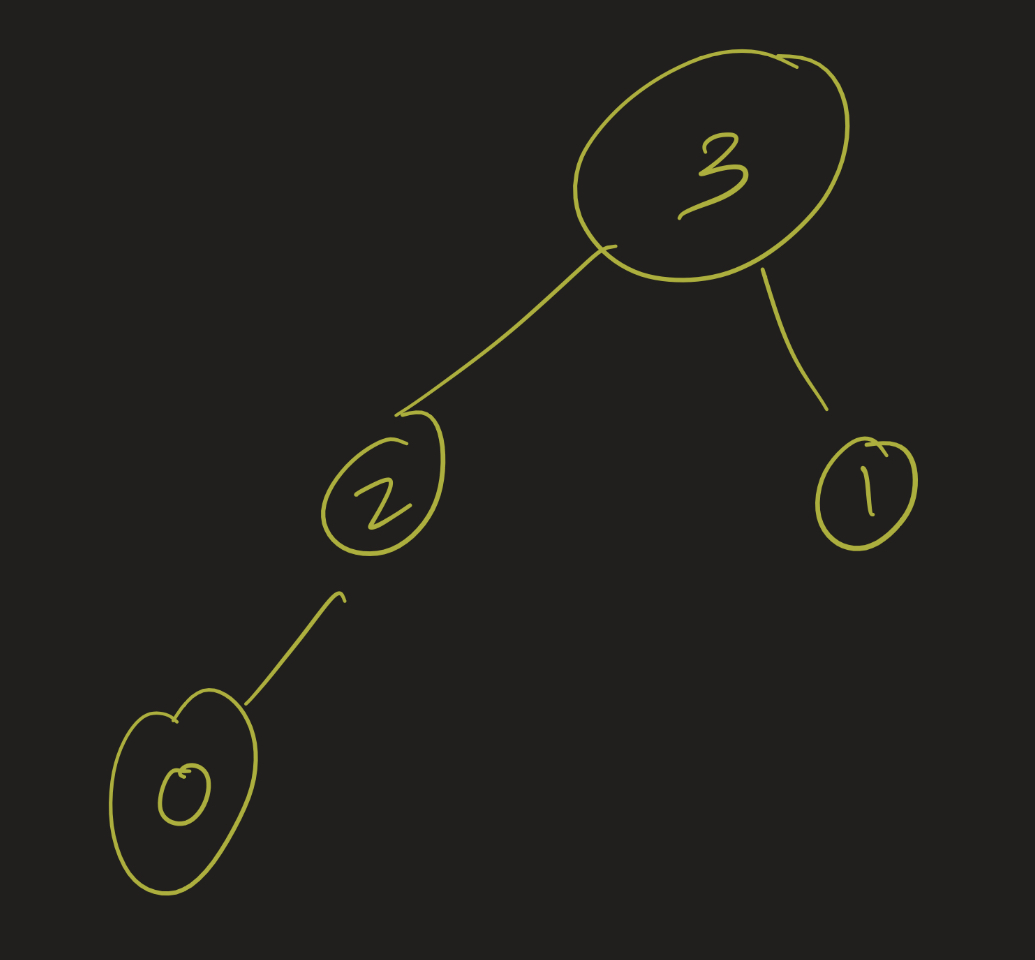
Color vertices in order. How many colors?

Topics

• Other kinds of trees: Red-Black trees, B-trees, 2-3-4 trees, splay trees: Describe the data structure. Prove the running times. Explain what they are used for (don’t need to do all of these, maybe just one, or maybe more?)
• Huffman Coding (compression). Describe the compression algorithm and give a thorough explanation of the data structures used in it (the “trie” data structure). Implement the algorithm and run it on a large file (\(>2\)MB). How much does it actually compress that file?

Topics

• Union-find algorithm / Disjoint Set data structure. Explain the problem and the data structure. Explain how this data structure can be used to help solve the “Synonymous Search Queries” question in the case where the synonym relation is transitive.
• Heuristic algorithms for NP complete problems. Take your favorite NP-complete problem (not graph coloring), and describe an algorithm which attempts to solve it. Describe its running time and the scenarios for which this algorithm will work well.

Topics

• Data structures used in Operating System design
• Find the Longest Common Substring of a set of words. Explain the algorithms and their running times. There is an algorithm which uses “suffix trees”: describe how to implement this data structure and how it helps solve the problem.
• “Median of medians” pivot selection strategy. Explain the algorithm, show some examples, and implement it. Prove that this strategy results in a worst case \(O(n)\) quickselect algorithm (and worst case \(O(n \log(n))\) quicksort).

Topics

… or any other problem you’ve seen that was interesting and that you’d like to explore in more depth.

• Try to rank your preferences and let me know by Friday.
• I will try to use that to make groups
• Let me know if you have made groups already.
• Then as a group you will need to come to a consensus.

External Sort

Changing the description:

• 12GB of data on disk
• 4GB of RAM
• Output to a new file on disk

Ideas?

HW 3

• HW 3 grades are posted for most.
• If you submitted multiple files, I did not grade it.
• Re-submit as a single PDF file!

Pivot Selection schemes

• Pick the first element as a pivot. Worst case: the list is already sorted!
• Pick the last element as a pivot. Worst case: still, if the list is sorted (or in reverse order).
• Pick a random pivot. Worst case: you’re just really unlucky. Perhaps this is good enough?

We will study some other possible improvements.

Median of 3

Make the pivot be the median of three elements. Two simple implementations:

1. Find the median of the first, last and middle elements.
2. Find the median of three random elements.

The worst case here is still \(O(n^2)\)! But it’s somewhat less likely to happen, and on average the random version improves on the number of comparisons that the “random pivot” strategy would make.

Dual pivots

The version currently implemented in the Java standard library Arrays.sort, created by Vladimir Yaroslavskiy, Jon Bentley, and Joshua Bloch, uses two pivots. Idea:

1. Pick pivots \(p_1\) and \(p_2\) with \(p_1 < p_2\).
2. Partition the list into three parts: the part less than \(p_1\), the part in between \(p_1\) and \(p_2\), and the part greater than \(p_2\). At this point, \(p_1\) and \(p_2\) should be in the correct positions.
3. Quicksort the three parts.

Caveat

Technically, the one in the JDK is much more complicated, but this is the spirit of the algorithm.

• Small arrays: uses insertion sort instead.
• “Close” to being sorted, mergesort is used.
• Non-primitives: “Timsort”

Quickselect

Recall the selection problem: given an unsorted list and an integer \(k\), find the \(k\)-th largest element. We can use a variant of quicksort, called quickselect, to solve this problem:

1. Pick a pivot (for now, let’s pick a pivot randomly).
2. Partition the list and determine the \(pivotIndex\), the position of the pivot.
3. If \(k == pivotIndex\), return the pivot.

Otherwise? Recursion!

Quickselect

4. If \(k < pivotIndex\), run quickselect on the list from \(start\) to \(pivotIndex - 1\).
5. If \(k > pivotIndex\), run quickselect on the list from \(pivotIndex + 1\) to \(end\), searching for \(k - pivotIndex - 1\).

Example

Find the 3rd largest element of the following list: [3, 1, 4, 5, 9, 2, 6]

• Pick pivot = 3 (randomly)
• Partition: [2, 1, 3, 5, 9, 6, 4]
• Index = 2, quickselect([5, 9, 6, 4], 0)
• Pick pivot = 4 (randomly)
• Paritition: [4, 9, 6, 5]
• Index = 0: returns 4!

Running time

Worst case: \(O(n^2)\). Proof?

Best case: each partition takes \(m\) comparisons (really \(O(m)\), but we will simplify), where \(m\) is the size of the part of the array that we are looking at. If the pivot is the median every single time, then the number of comparisons needed is:

\[n + n / 2 + n / 4 + \ldots = 2n\]

which is \(O(n)\).

Average case analysis

Average case? This is the scenario where every pivot is equally likely.

Let \(T(n, k)\) be the expected time to find the \(k\)-th smallest in an array of size \(n\), and \(T(n)\) be the largest value over all \(k\).

• It takes \(n - 1\) comparisons to partition the array.
• The array is split into pieces: \(0\) and \(n - 1\), \(1\) and \(n - 2\), etc. We assume here that we always pick the larger piece.

Magic

\[T(n) \leq n - 1 + average(T(n / 2), \ldots, T(n - 1))\]

Magic: prove that \(T(n) \leq 4n\) by induction.

• True for \(T(0), T(1), T(2)\) by inspection.
• Assume that, for all \(i < n, T(i) \leq 4i\).
• Using the equation above, we get:

\[ \begin{align} T(n) &\leq n - 1 + average(4(n / 2), \ldots, 4(n - 1)) \\ &= n - 1 + 4(3n / 4) < 4n \end{align} \]

So \(T(n) = O(n)\).

Bucket Sort

Keep 100 “buckets”. Run through the list and add to a counter. Then run through all the buckets and output them all.

Suppose there are \(N\) numbers and \(M\) buckets. What is the running time?

Radix Sorting

What if \(N\) is much smaller than \(M\)? In particular: how do we sort \(10\) elements that are all between \(1\) and \(999\)? Two ideas:

• “Most significant digit” sorting: sort by the hundreds digit, then tens digit, then ones.
• “Least significant digit” sorting: sort by 1s digit, then 10s, then 100s.

Important: each step must be stable.

Exercise: try this out on 125, 111, 061, 209, 290, 095.

Exercise

Consider an \(n\) by \(n\) matrix \(M\), whose rows and columns are each sorted in increasing order. That is, the elements of each row increase as you go left to right, and the elements of each column increase as you go down. Determine if a number \(x\) is in the matrix in \(O(n)\) comparisons.

Homework

2. Given an array of \(5\) elements, what is the probability that the worst case for quicksort actually happens? That is, what is the probability that every pivot we select happens to be either the largest or smallest possible element? What if the array has \(10\) elements?

Homework

3. Describe an algorithm (in English or pseudocode) which uses at most 7 comparisons to sort an array of 5 elements.
4. Sort 3, 1, 4, 1, 5, 9, 2, 6 using mergesort. Show every step.