Pseudocode

public void percolateDown(int i) {
  num = array[i]
  child = 2*i + 1
  while (child < tail) {
    if (child + 1 < tail && array[child] > array[child+1]) {
      child++
    }
    if (array[child] < num) {
      slide array[child] up
      update i, child
    } else {
      break
    }
  }
  array[i] = num
}

Sum of heights

• Definition: the height of a node is the length of the longest path from that node to a leaf.
• Each node has to go “down” by, at most, its height.
• Each step it goes down: at most 2 comparisons.
• Therefore: at most \(2 \times height\) comparisons.
• What is the sum of the heights of a complete binary tree?
  • Let’s do 3 examples: \(n = 11\), \(n = 12\), \(n = 16\).
  • Something to do with the binary representation of the number.

Representations

• An adjacency list for a vertex is the list of all the vertices it shares an edge with.
• An adjacency matrix is an \(n \times n\) matrix such that the \((i, j)\) entry is \(1\) if there is an edge between \(v_i\) and \(v_j\), and \(0\) if there is no edge.
  • If we want to represent weighted graphs?

Adjacency List

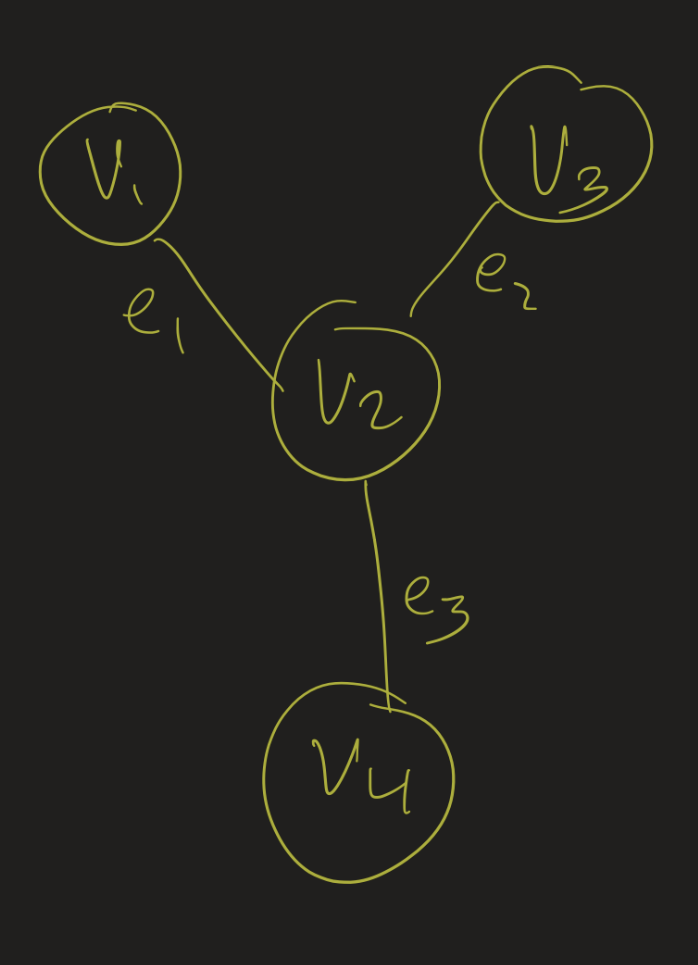
Adjacency Matrix

Code

public class Graph {
  private boolean[][] adjacencyMatrix;

  public Graph(int n) {
    adjacencyMatrix = new boolean[n][n];
  }
  
  // puts an edge between vertices i and j
  public void makeEdge(int i, int j) {
    adjacencyMatrix[i][j] = true;
    // should this be symmetric?
  }
}

More Graph Theory

A \(k\)-clique is a group of \(k\) vertices that all are mutually interconnected. A \(k\)-anti-clique is a group of \(k\) vertices such that none of them are connected to each other.

Theorem: Every graph with at least 6 vertices has either a 3-clique or a 3-anti-clique.

Proof? Corollary (in terms of friendship)?

Example

Look for the “steady-state” vectors here. How?

Video

BFS Pseudocode

Queue<Vertex> q;
setAllDistancesToInfinity()
s.dist = 0
q.enqueue(s)
while (!q.isEmpty()) {
  Vertex v = q.dequeue()
  v.visited = true
  for (Vertex w : v.getAdjacentVertices()) {
    if (!w.visited) {
      if (v.dist + 1 < w.dist) {
        w.dist = v.dist + 1
        w.parent = v
        q.enqueue(w)
      }
    }
  }
}

Weighted Graphs?

• Above idea needs to be modified.
• Instead of just adding 1, you need to add the weight.
• When you take from the “queue”, you want to take off the node that has the shortest current distance.
  • Not FIFO! So: use a priority queue!
• This is the idea behind Dijkstra’s Algorithm

Pseudocode

initializeDistances()
pq.insert(s)
while (!pq.isEmpty()) {
  Vertex v = pq.removeMin()
  v.visited = true
  for (Vertex w : v.getAdjacentVertices()) {
    if (!w.visited) {
      if (v.dist + weight(v, w) < w.dist) {
        w.dist = v.dist + weight(v, w)
        w.parent = v
        pq.insert(w)
      }
    }
  }
}

Implementation details

• We may end up inserting a vertex multiple times in this algorithm.
• But at the end, the distances and parents will be correct.
• Instead of v.visted = true, might have a Set object.
• parent and dist might be Maps instead of properties in the Vertex class.
  • Might not even have a Vertex class.

decrease-key

• Instead of re-inserting: you could just change the “priority” of \(w\)
• That is: check if \(w\) is in the priority queue, and if so, change its priority.
• How would we find \(w\) in the priority queue quickly?

Video

Aside: Dijkstra

• Edsger Dijkstra: famouse Dutch computer scientist.
• Dijkstra’s algorithm: 1956, published 1959
• Besides Dijkstra’s algorithm, most famous for his paper: “GOTO Statement Considered Harmful” (1968)
• Launched a series of responses / memes (“‘GOTO Considered Harmful’ Considered Harmful”, “‘“GOTO Considered Harmful” Considered Harmful’ Considered Harmful?”)
  • Dijsktra (May 1987): “On a Somewhat Disappointing Correspondence”

2. Prove that for binary heaps, buildHeap (where we take an array of \(N\) integers and turn it into a heap, in-place) does at most \(2N - 2\) comparisons between elements.

• Recall: buildHeap: start at the “end” of the heap, “percolateDown” each element.
• Each “move” requires 2 comparisons.
• Each node may move as much as its height.
• Sum of the heights of all nodes? (Prove it’s \(\leq N - 1\))
• Hint: something to do with the number of ones in the binary representation of \(N\).

3. Show that a heap of eight elements can be constructed in eight comparisons between heap elements. (Not obvious!)
4. Write pseudocode which, given an adjacency matrix for a graph and vertices i and j, whether there is a path between i and j.