Data Structures Lesson 14
Professor Abdul-Quader
Intro to Graphs
Project 2
Questions?
Benchmarking in Java
Complications:
- JVM “warmup”: class loading, JIT compiling
- Garbage Collection
Do you need to handle all of these? No. But some of these could explain strange results.
Quiz 1
sort:
- insert into the tree, one by one
- Then call sort()
- Running time?
Obviously?
- Is this obvious?
- Without thinking: insert is \(O(\log N)\), we do that N times…
- Plus running time of sort.
Deeper?
- Each time we insert, the size changes.
- Let’s be more precise?
buildHeap
- Pseudocode?
- Running time? How many comparisons needed
Overlapping Intervals
A website earns advertising money (per viewer) based on the number of minutes a viewer spends visiting their website. The website only tracks when a browsing session starts and ends.
Continued
A user may have multiple browsing sessions open at the same time (multiple facebook tabs open), and the browsing sessions might not be ordered in any way. How can we tally up the minutes a user spends?
Format
The format for the data is a list of intervals: (start1, end1), (start2, end2), \(\ldots\), (start100, end100). This list can be given in any order.
Ideas?
Graphs
A graph is a set of vertices and edges: \(G = (V, E)\). An edge is a pair of vertices. Graphs can be either undirected or directed. If a graph is directed, edges have a start vertex and end vertex (usually represented by arrows).
Graph Questions
Graphs are incredibly useful mathematical abstractions. There are many questions one can think about:
- How can we represent graphs?
- How can we tell if two vertices are connected by an edge?
- How can we tell if there is a path between two vertices?
- etc.
Definitions
- degree of a vertex: the number of vertices it is connected to.
- In a directed graph, we can define in-degree and out-degree
- Edges can be weighted: for example, to represent the distance between two cities on a map.
Weights can come into play when dealing with “shortest path” questions.
Representations.
Let \(G = (V, E)\) be a graph. Suppose \(V = \{ v_1, v_2, \ldots, v_n \}\) (so it has \(n\) vertices).
- An adjacency list for a vertex is the list of all the vertices it shares an edge with.
- An adjacency matrix is an \(n \times n\) matrix such that the \((i, j)\) entry is \(1\) if there is an edge between \(v_i\) and \(v_j\), and \(0\) if there is no edge.
- If we want to represent weighted graphs?
Adjacency List
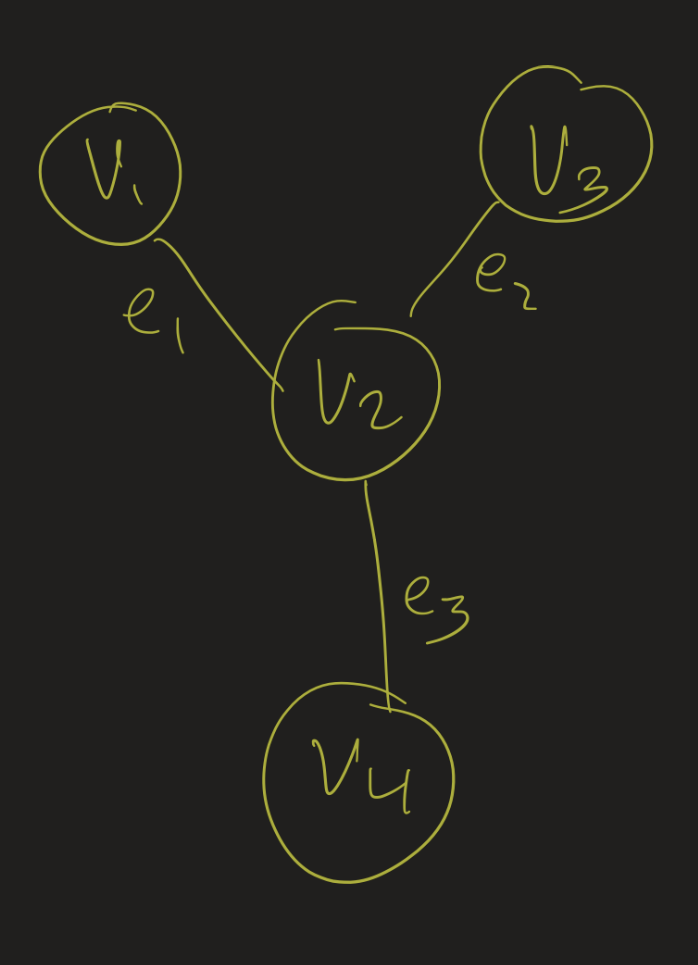
Adjacency List:
- \(v_1\): \(v_2\)
- \(v_2\): \(v_1, v_3, v_4\)
- \(v_3\): \(v_2\)
- \(v_4\): \(v_3\)
Adjacency Matrix

\[ \begin{array}{c|c|c|c|c} & v_1 & v_2 & v_3 & v_4 \\ \hline v_1 & 0 & 1 & 0 & 0 \\ v_2 & 1 & 0 & 1 & 1 \\ v_3 & 0 & 1 & 0 & 0 \\ v_4 & 0 & 1 & 0 & 0 \end{array} \]
Graph Theory
Simple graph theory result:
Theorem: Every finite, undirected graph has an even number of vertices with odd degree.
Proof?
Corollary: in every group of people, there is an even number of people who have an odd number of friends.
More Graph Theory
A \(k\)-clique is a group of \(k\) vertices that all are mutually interconnected. A \(k\)-anti-clique is a group of \(k\) vertices such that none of them are connected to each other.
Theorem: Every graph with at least 6 vertices has either a 3-clique or a 3-anti-clique.
Proof? Corollary (in terms of friendship)?
PageRank
Application: Google’s PageRank algorithm.
- \(N\) websites.
- Each website may / may not have a link to the other sites.
- “Ranking” algorithm: try to figure out, if a user randomly clicks links, in the limit, what is the probability that they end up on page \(i\)?
- Solution: Linear Algebra.
Example
Simplified internet with just 4 websites.
- Page 1 has links to pages 2, 3, and 4
- Page 2 has a link to page 4
- Page 3 has links to pages 1 and 4
- Page 4 has links to pages 1 and 3
Represent with the following matrix:
\[ \begin{pmatrix} 0 & 0 & .5 & .5 \\ 1/3 & 0 & 0 & 0 \\ 1/3 & 0 & 0 & .5 \\ 1/3 & 1 & .5 & 0 \end{pmatrix} \]
Look for the “steady-state” vectors here. How?
Upcoming
- Project 2 due Friday
- Presentations 3/31 and 4/3
- Quiz 2 after break
- HW 3 assigned over break?