Think about

As we learn about these, keep this question in mind: in what scenarios (in terms of the table size \(s\) and the number of insertions \(N\)) might we prefer one scheme over the other?

Load Factor

• Let \(N\) be number of elements to insert into the table.
• Let \(s\) be the size of the table.
• \(\lambda = \dfrac{N}{s}\) is called the load factor of the table.
• \(\lambda\) small: few collisions, lots of wasted space
• \(\lambda\) large: space used efficiently, but high chance of collisions.

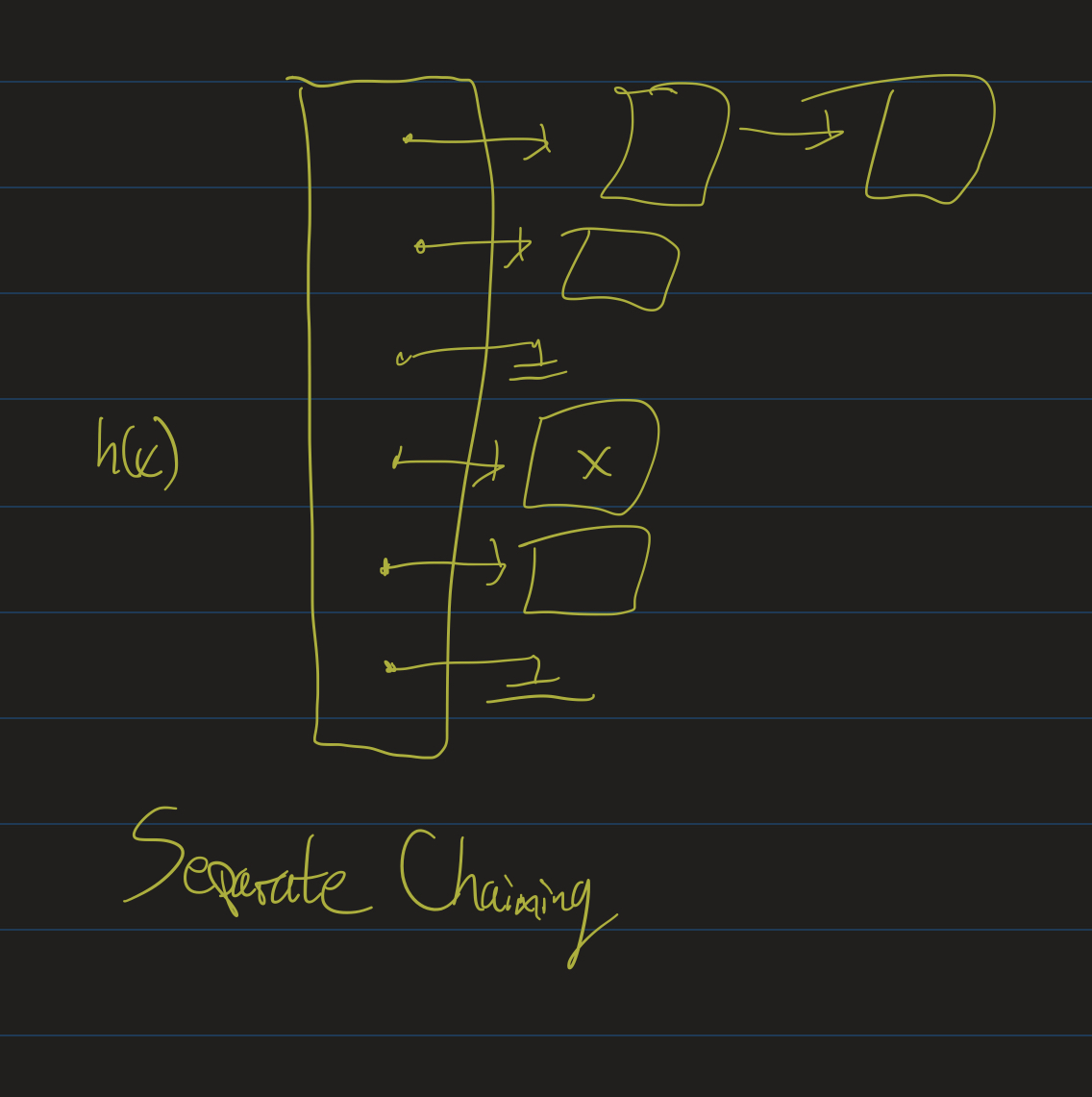
Separate Chaining

• Don’t keep a “large array”.
• Instead: keep an array of \(s\) lists.
• Think of each list as a “bucket” (or “bin”).
• Elements that hash to the same value go in to the same bucket.

Image

Running times

• Insert \(x\): compute hashcode \(h(x)\), add \(x\) to the \(h(x)\)-th list.
• Running time of insert?
• contains: compute the hash function, check the relevant list.
• Running time (average case)? Worst case?
• What happens as \(\lambda\) increases?
• Can we keep a bound on \(\lambda\)?

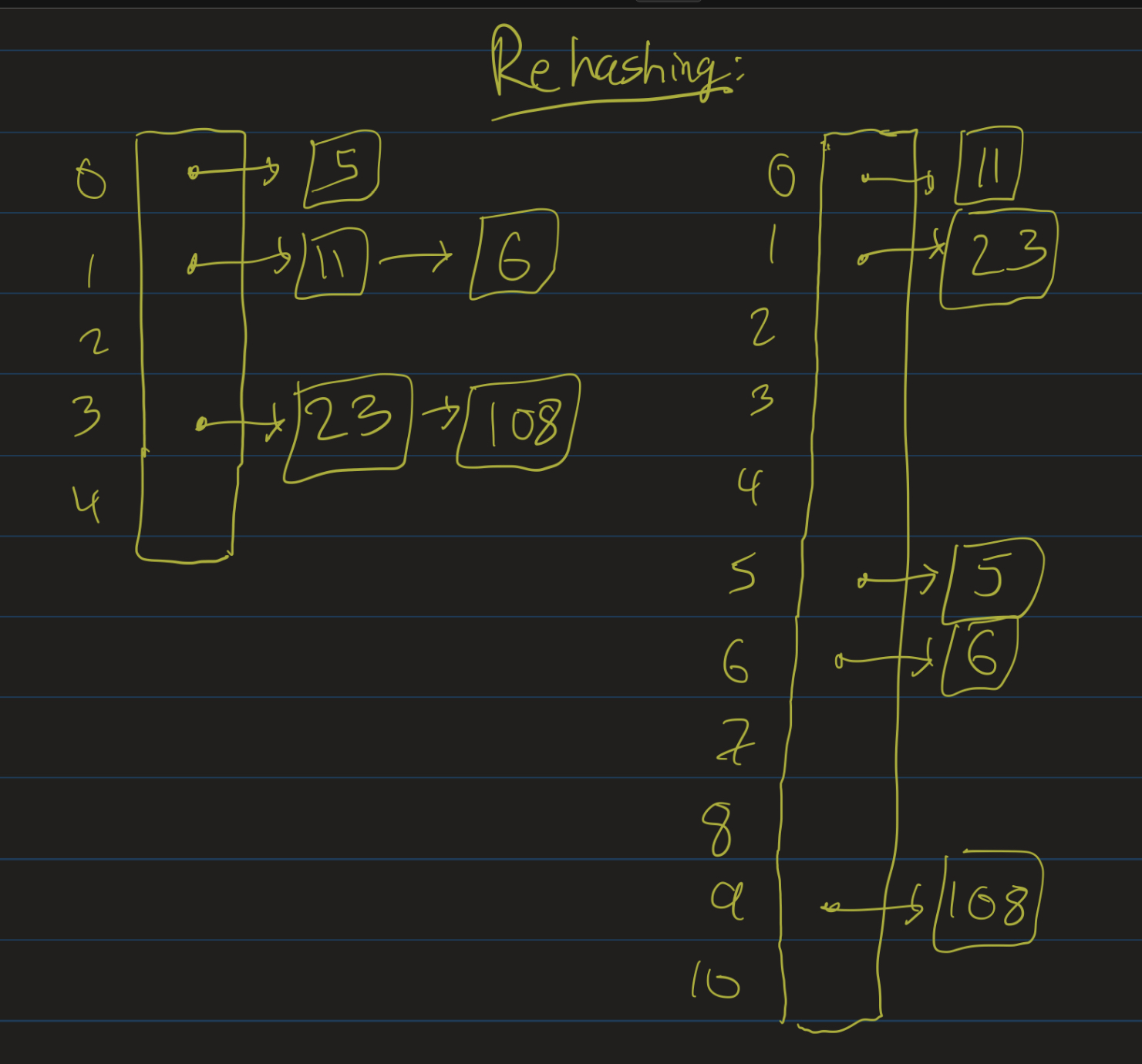
Rehashing

• If we allow \(\lambda\) to increase without bound, performance degrades.
• Many implementations (including Java’s) will rehash if it increases too much.
• Increase the size of the table (usually: pick the next prime number \(p > 2s\)).
• Go through each previously inserted item, and re-insert into the new table.
• Should not happen too often, so that we still get (amortized) constant time inserts.

Image

Video

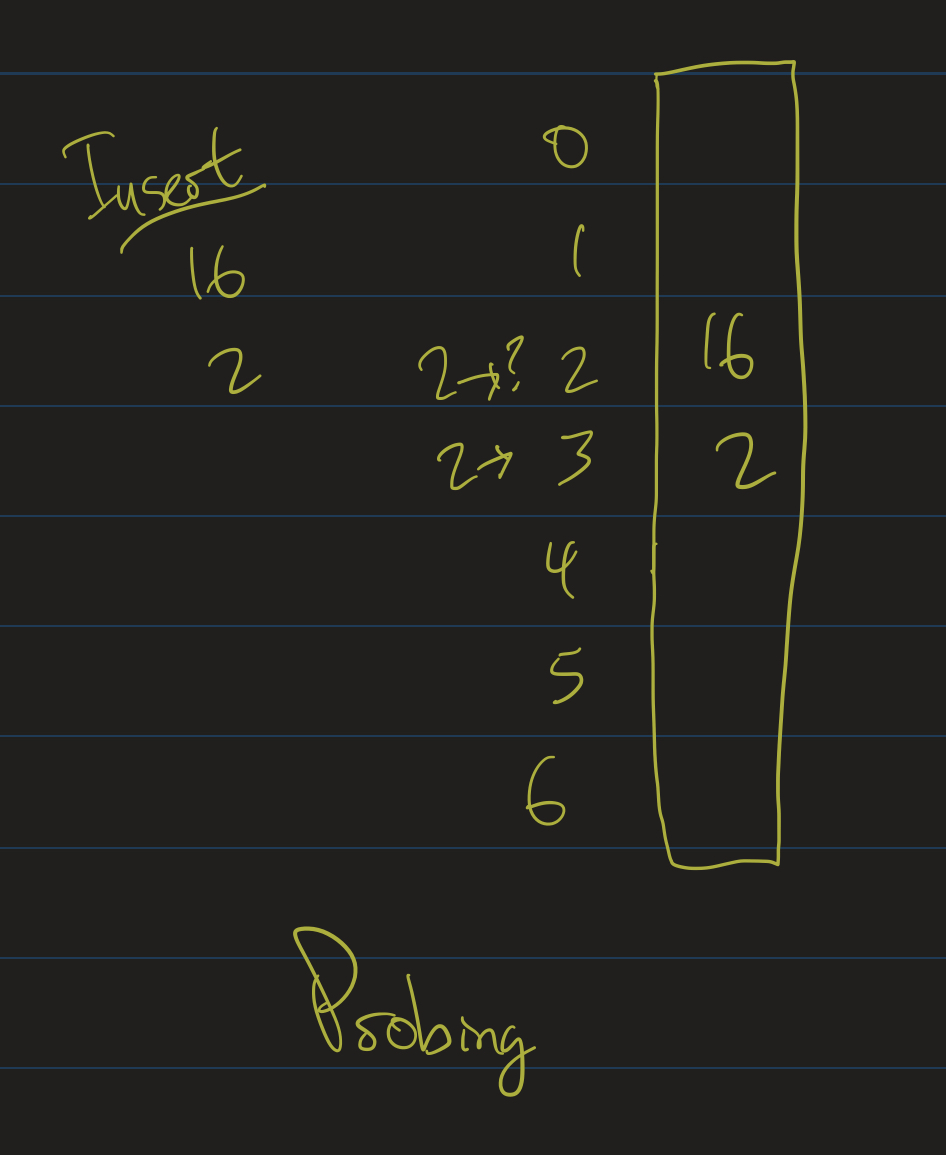
Example

• Table size = 7, insert 16 and 2.
• 16 mod 7 = 2, so put 16 at position 2.
• 2 mod 7 = 2, so try to put 2 at position 2.
• Fails, so check position 3.

Image

More generally

• Let \(h(x)\) be our hash function.
• Use another function, \(f(i)\), callled collision resolution function.
• Consider the sequence \(h(x) + f(0), h(x) + f(1), h(x) + f(2), \ldots\)
• Above: \(f(i) = i\).
• \(f(i)\) linear: linear probing.
• \(f(i)\) quadratic: quadratic probing.
• Both cases: want \(\lambda\) to be small, usually less than 0.5

Analysis (Linear)

• If \(s > N\), can always find a spot.
• Might take too long!
• clustering: tendency of keys to cluster around a few spots.
  • Too many objects hash close to each other.
  • Clustering leads to more clustering
• Average # probes for insert / unsuccessful search: \(\frac{1}{2}(1 + \frac{1}{(1 - \lambda)^2})\).
• Average # probes for successful search: \(\frac{1}{2}(1 + \frac{1}{1 - \lambda})\).

Video

Problem

• 14 mod 7 = 0. Taken.
• 0 + 1 = 1. Taken
• 0 + 4 = 4, Taken.
• 0 + 9 = 9 mod 7 = 2. Taken.
• 0 + 16 = 16 mod 7 = 2.
• 0 + 25 = 25 mod 7 = 4.
• 0 + 36 = 36 mod 7 = 1.

Modular arithmetic is cyclical: anything over \(f(6)\) will repeat. Never find an open spot!

Upshot

• If \(\lambda > 0.5\) or \(s\) is composite, it’s possible we don’t find an open spot to insert!
• Necessary that \(\lambda \leq 0.5\) and \(s\) is prime.
• Theorem: In that case (\(\lambda \leq 0.5\) and \(s\) is prime), you will always find a spot to insert into the table.

Removals

• \(s = 7\).
• insert(2), insert(16)
• remove(2)
• contains(16)?
• Do you see the problem?

Lazy Deletion

• Lazy deletion: Keep a flag for whether or not a cell is deleted.
• Don’t actually set the entry to null!
• If we search for 16
  • Check position 2.
  • If it’s null, not there.
  • Otherwise, something was there: probe until we see null (or 16).

Image

Video

Map ADT

• Asks the question: why must arrays use integer indices?
• map: a set of key-value pairs.
• void put(K key, V value)
• V get(K key)
• boolean containsKey(K key)

Example

HashMap<String, Integer> namesToAgesMap = new HashMap<>();
namesToAgesMap.put("Bob", 27);
namesToAgesMap.put("Athar", 29); // yeah right
namesToAgesMap.put("James", 55);

// some other code
public int getAge(Map<String, Integer> agesMap, String name) {
  if (agesMap.containsKey(name)) {
    return agesMap.get(name);
  }
  // if we don't know their age:
  return -1;
}

Implementations

• Standard library provides good implementations of Map and Set interfaces
  • TreeSet, TreeMap, HashSet, HashMap
• Generic! Works with any class.
• BUT: you must implement equals and hashCode

equals / hashCode

• equals(Object o): returns true if o is “equal” to your object
• hashCode(): two objects that are “equal” must return the same hashCode
  • Otherwise, HashMap might not work correctly!
  • If-then: if they are equal, hashCode should be equal. Other way around? Not necessary.
  • hashCode should be random. Distribute objects uniformly across integers.

Algorithms

• Simple \(O(n^2)\) solution using nested for loops.
• Pseudocode?
• Improve it using a data structure?
• Pseudocode and running time of improved solution?

Hint

Level-order traversal:

enqueue(root)
while (queue is not empty) {
    dequeue a node
    print node.data
    enqueue node.left, node.right
}

Modify this algorithm to keep track of the path from the root to the node?

Hint 2

• Each node should keep track of who enqueued it.
• Modify the while loop to exit as soon as you dequeue the node you’re looking for.
• Then backtrack.
• Code here is tricky: try to implement this!