Calculus I Lesson 8: Higher Order Derivatives

1. Warm Up
   1. x = 0
   2. x = 1 Differentiable?
   3. x = 1 Continuous?
   4. x = 2
   5. Graph
2. Higher Order Derivatives
   1. Physics Example
   2. Crime Example
   3. COVID-19
3. Tangent Lines
   1. Graph
   2. Meaning of “Tangent Line”
4. Reminders

Warm Up

\[f(x) = \begin{cases}x^2 - 1 &\mbox{if } x < 1 \\ x - 1 &\mbox{if } x \geq 1 \end{cases}\]

Is $f(x)$ differentiable, continuous, both, or neither at the following points:

• $x = 0$
• $x = 1$
• $x = 2$

x = 0

$x^2 - 1$ is differentiable at $x = 0$. Therefore it is also continuous.

Answer: Both

x = 1 Differentiable?

Need to check left and right hand limits of

\[\lim_{x \rightarrow 1} \frac{f(x) - f(1)}{x - 1}\]

From the left: $\dfrac{(x^2 - 1) - 0}{x - 1} \rightarrow x + 1 \rightarrow 2$.

From the right: $\dfrac{x -1 - 0}{x - 1} \rightarrow 1$. Not differentiable

x = 1 Continuous?

Now we check if $f(x)$ is continuous at $x = 1$:

• $f(1) = 0$
• ${\displaystyle\lim_{x\rightarrow 1^-}} f(x) = {\displaystyle\lim_{x \rightarrow 1^-}} x^2 - 1 = 0$
• ${\displaystyle \lim_{x\rightarrow 1^+}} f(x) = {\displaystyle \lim_{x \rightarrow 1^+}} x - 1 = 0$.

So $f$ is continuous at $x = 1$.

x = 2

$x - 1$ is differentiable, its derivative is $1$ near $x = 2$. Differentiable functions are continuous, so both.

Graph

Higher Order Derivatives

Given a function $f$:

• $f^\prime$: first derivative of $f$ with respect to $x$
  • represents “How fast $f$ is changing at each $x$”
  • positive / negative / 0?
• $f^{\prime\prime}$?: second derivative
  • How fast is $f^\prime$ changing?
  • How fast is $f$ accelerating?
• $f^{\prime\prime\prime}$?
• $f^{(n)}$ ($n$-th derivative)?

Physics Example

• Ball thrown straight in the air. $t$ = seconds, $h$ = meters
• $h(t) = -5t^2 + 20t + 2$ meters, $t$ seconds after it is thrown
• What does $h^\prime(t)$ mean?
• What does $h^{\prime\prime}(t)$ mean?

Crime Example

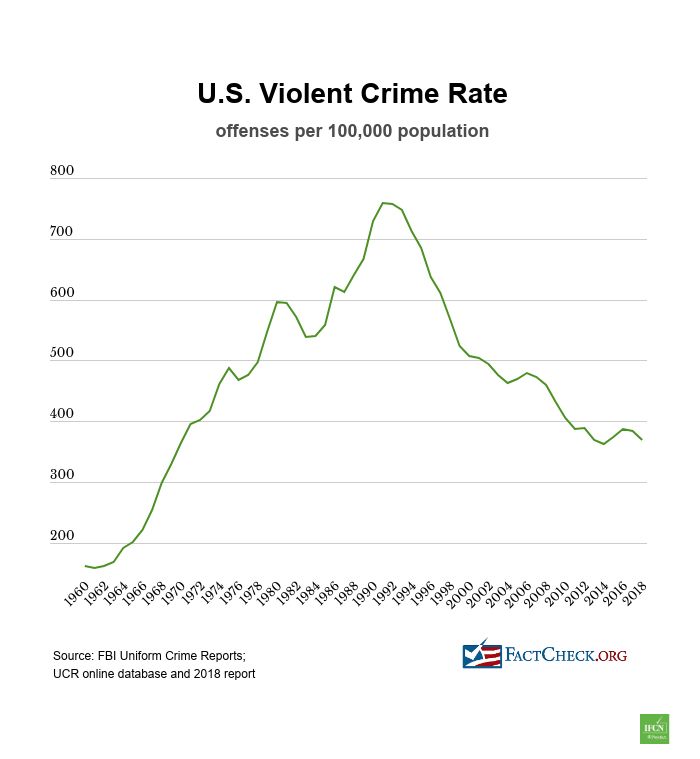
This graph shows the US Violent Crime Rate over time.

• What does the derivative of this graph represent?
• What does the second derivative of this graph represent?

COVID-19

Take a look at the following graphs.

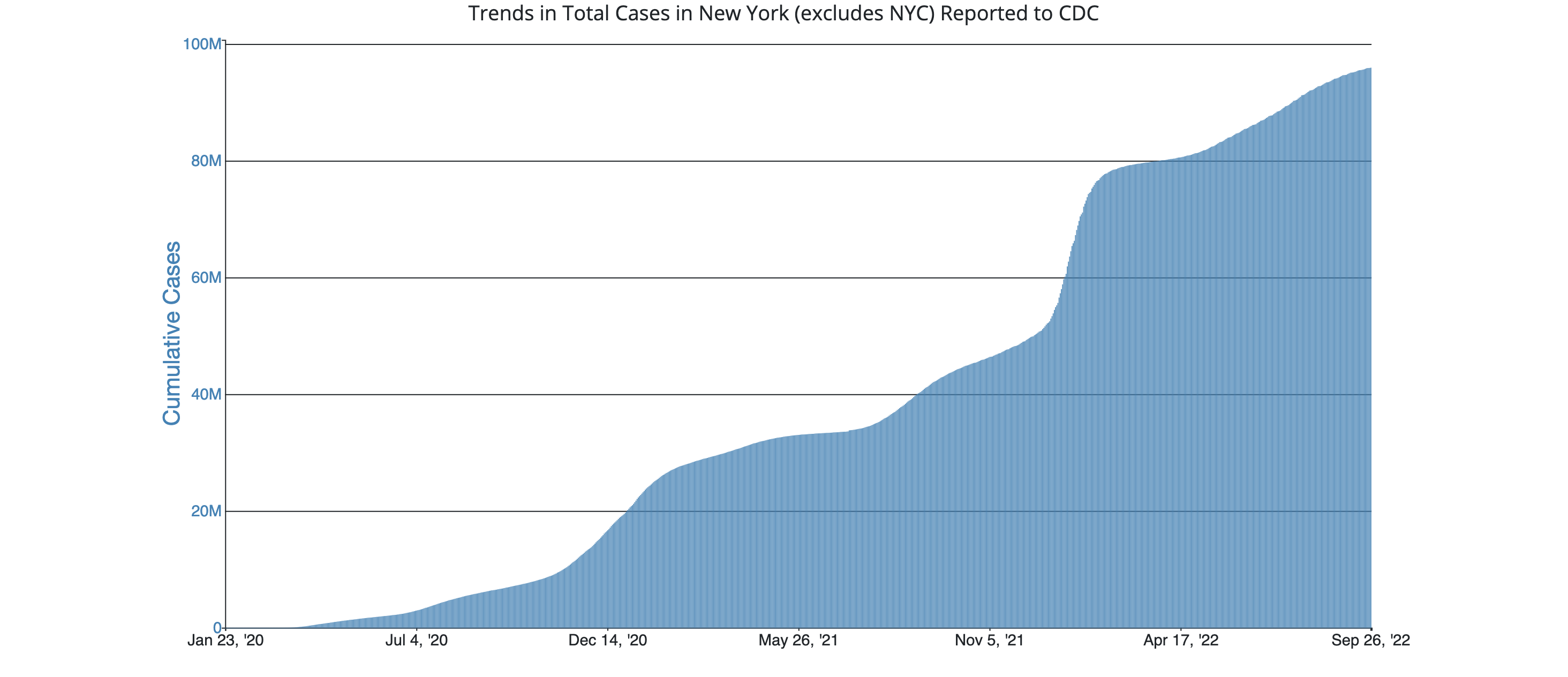
Graph 1: total COVID cases in NY (excluding NYC) over time:

Graph 2: daily COVID cases in NY (excluding NYC) over time:

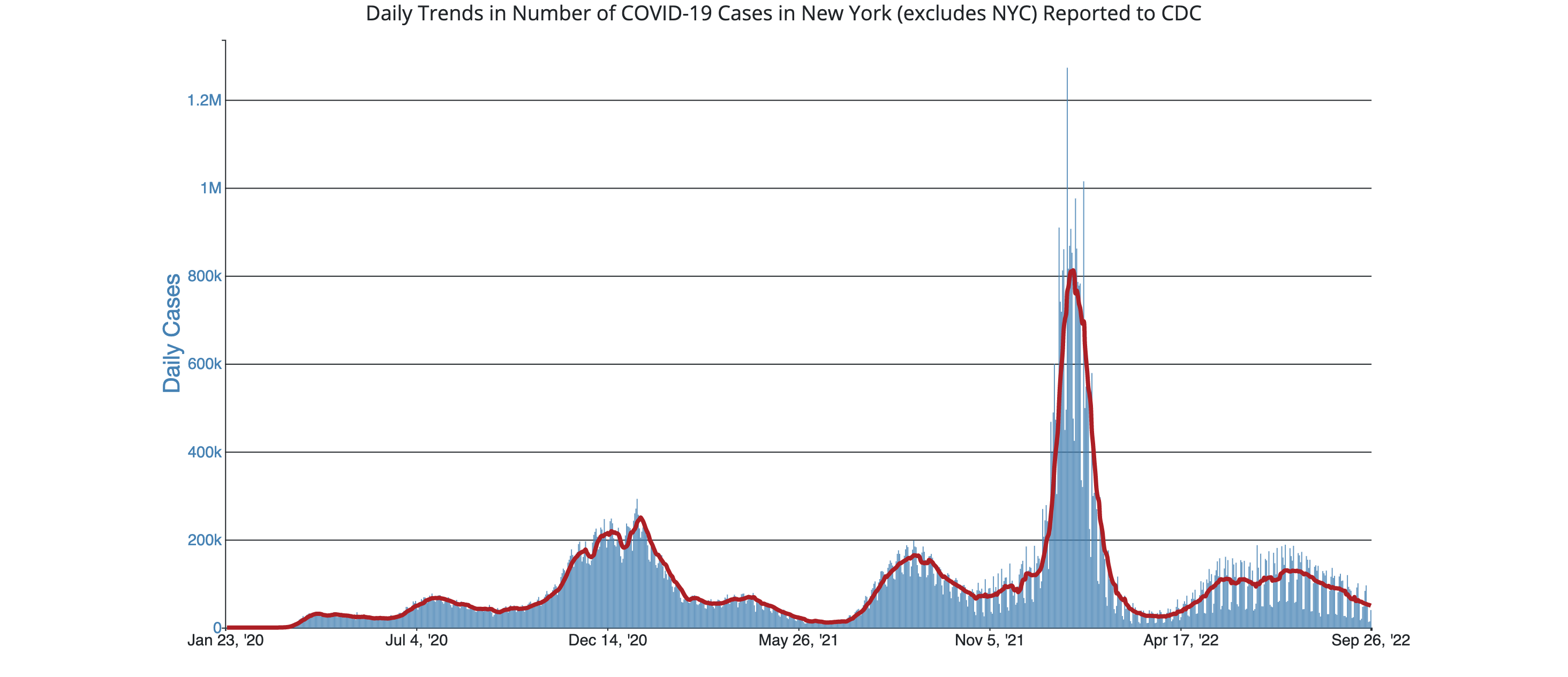
What does the derivative of each of these graphs represent? What stands out to you about these derivatives?

Tangent Lines

Recall that we defined the derivative to mean: “the slope of the tangent line”. How do we actually figure out what that tangent line is?

Problem: Find the equation of the line tangent to $y = x^3 - 2x$ at $x = 1$.

Recall: point-slope form: $y - y_0 = m(x - x_0)$

• Point: $(x_0, y_0)$ is $(x, f(x))$
• Slope: $m = f^\prime(x)$

So how do we find the equation? First find the point. Since we’re looking at $x = 1$, we plug in to find $y = 1^3 - 2(1) = -1$, so the point is $(1, -1)$.

Now let’s find the slope by taking the derivative. We want the slope at $x = 1$, so we look for $f^\prime(1)$. First find the derivative: $y^\prime = 3x^2 - 2$. At $x = 1$: $3(1)^2 - 2 = 1$.

So our equation is: $y + 1 = 1(x - 1)$, or $y + 1 = x - 1$. Or $y = x- 2$

Graph

Meaning of “Tangent Line”

What does the “tangent line” even mean? The idea is that it’s the best “linear approximation” of $f(x)$ at $x = a$. In other words: zoom in close to $x = a$ on the graph. The closer we get, the more accurate the tangent line appears.

Reminders

• DeltaMath HW 4 due tonight.
• DeltaMath HW 5 due Monday.
• Exam 1 Monday:
  • One page of notes
  • Graphing Calculator allowed
  • Practice problems will be on BrightSpace tomorrow
  • Some multiple choice, some short answer
  • Sections 2.1 - 2.4, 3.1 - 3.4