Calculus I Lesson 23: Finishing Up; Definite Integrals / Substitution

1. Exam Recap
2. Definite Integrals of Rates
3. Review of Substitution
4. Computing Definite Integrals
   1. Method 1: Convert back to $x$
   2. Method 2: Update the bounds / keep $u$

Exam Recap

• Differentiable / continuous / both / neither
• Function analysis: increasing, decreasing, concavity
• Antiderivatives
• FTC, Chain Rule

Definite Integrals of Rates

Consider the following two graphs:

First: total COVID-19 cases in New York, excluding NYC (January 2020 - September 2022)

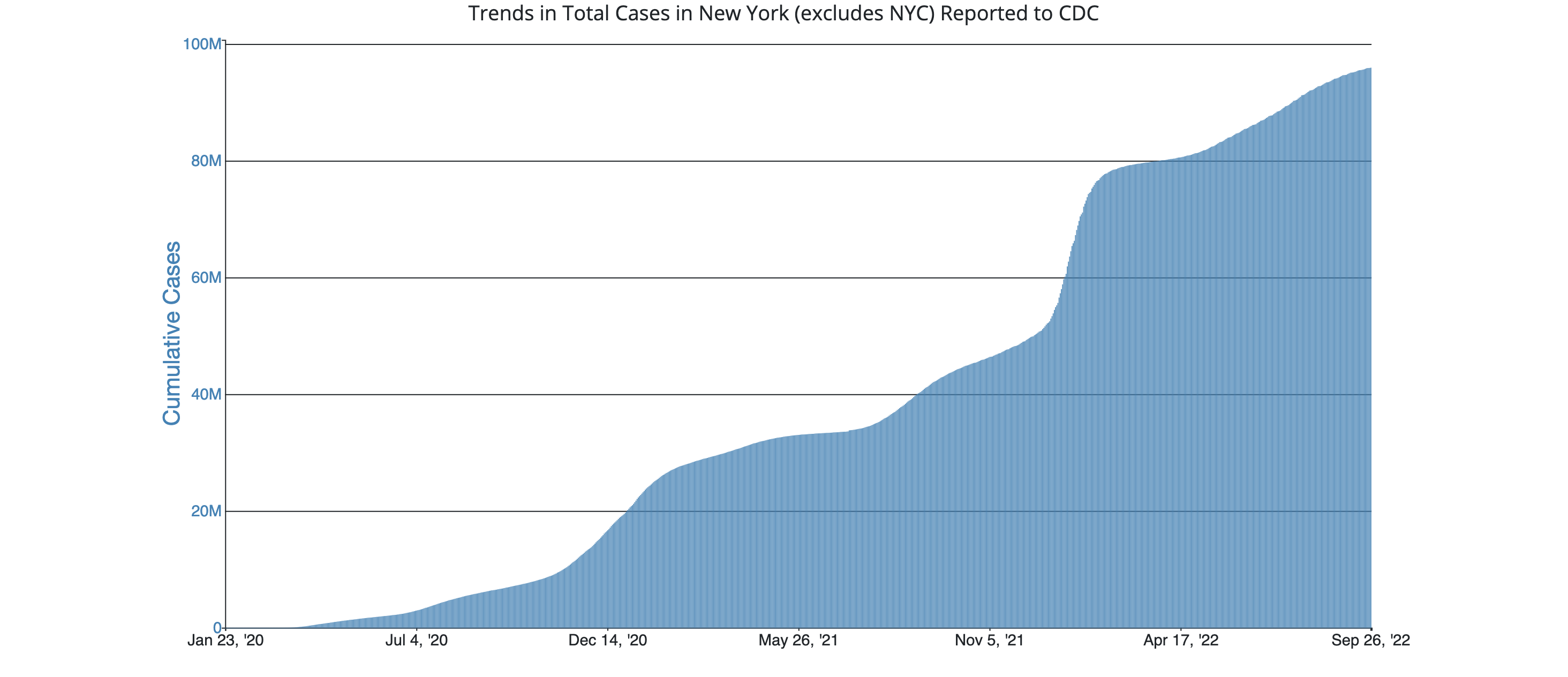
Second: daily COVID-19 cases in New York, excluding NYC (same time period):

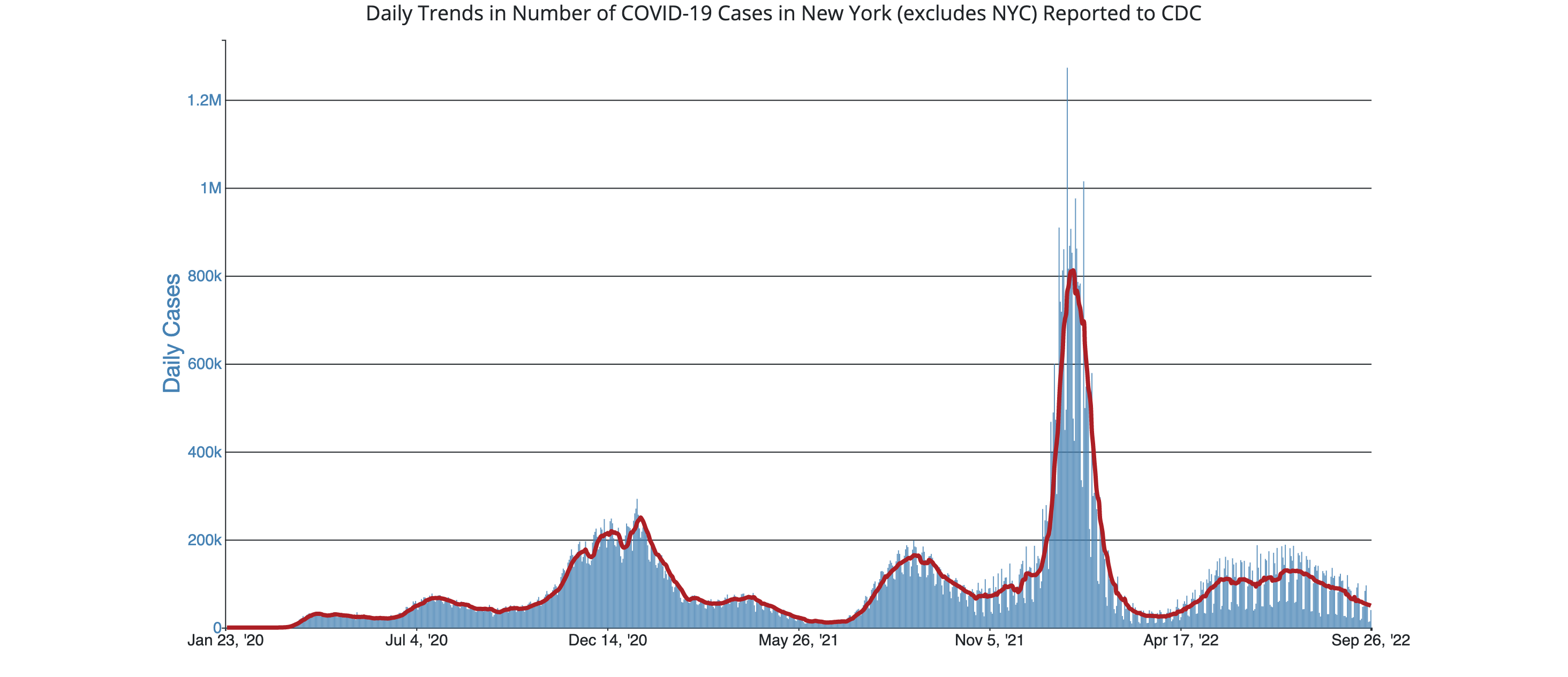
How do these two graphs relate to one another?

In general: if $f(t)$ is the rate of change in some quantity at time $t$, then $\int_a^b f(t) dt$ means the total change from $a$ to $b$ of that quantity. Examples:

• Water leaking from a tank at a rate of $R(t)$ liters per hour, then $\int_a^b R(t) dt$ is the amount of water that leaks out between $t = a$ and $t = b$ hours.
• Population increasing at a rate of $f(t)$ people per year, then $\int_a^b f(t) dt$ is the total increase in the population between year $a$ and year $b$.
• The COVID-19 graphs example above: what’s the rate, and what’s the accumulated quantity?

Review of Substitution

Today we will be using the method of integration by substitution in order to compute definite integrals. Before we do so, make sure you practice integration by substitution enough so that you get the hang of the technique.

Exercises: Use integration by substitution to find the following antiderivatives:

1. $\int \cot(\theta) d\theta$. Recall: $\cot(\theta) = \frac{\cos(\theta)}{\sin(\theta})$.
2. $\int \dfrac{x^2}{x^3 - 4} dx$
3. $\int \dfrac{e^{1/x}}{x^2} dx$.
4. $\int e^{2x + 1} dx$

Check your solutions.

1. Let $u = \sin(\theta), du = \cos(\theta) d\theta$. Then the integral is $\int \frac{1}{u} du = \ln(u) + C$. Substituting back, we get $\ln(\sin(\theta)) + C$.
2. Let $u = x^3 - 4, du = 3x^2$. This integral is $\frac{1}{3} \int \frac{1}{u} du = \frac{1}{3} \ln(u) + C = \frac{1}{3} \ln(x^3 - 4) + C$.
3. Let $u = \frac{1}{x}, du = -\frac{1}{x^2} dx$. This integral becomes $-\int e^u du = -e^u + C = -e^{1/x} + C$.
4. Let $u = 2x + 1, du = 2dx$. This integral becomes $\frac{1}{2} \int e^u du = \frac{1}{2} e^u + C = \frac{1}{2} e^{2x+1} + C$.

Exercises: For the following indefinite integrals, find an appropriate substitution (just determine $u$ and $du$) and set up the integral.

1. $\int x^4 \sqrt{x^5 - 1} dx$
2. $\int \frac{x}{\sqrt{1 - x^2}} dx$
3. $\int xe^{x^2} dx$

Check your solutions.

1. Let $u = x^5 - 1, du = 5x^4 dx$. This integral becomes $\frac{1}{5} \int \sqrt{u} du$.
2. Let $u = 1 - x^2, du = -2x dx$. This integral becomes $-\frac{1}{2} \int \frac{1}{\sqrt{u}} du$.
3. Let $u = x^2, du = 2x dx$. This integral becomes $\frac{1}{2} \int e^u du$.

As a side note, some integrals are not solvable using substitution. For example, $\int x^2 e^x dx$ is not solvable using substitution. $u = x^2$, $du = 2x dx$ does not work, and $u = x$, $du = dx$ does not help simplify the integral at all.

Exercises: Which of the following integrals are solvable using substitution?

1. $\int \ln(|\cos(x)|) \sin(x) dx$
2. $\int \dfrac{\ln(|\cos(x)|)}{\sin(x)} dx$
3. $\int \dfrac{\sin(x^2)}{x} dx$
4. $\int x\sin(x^2) dx$
5. $\int (\sin(x))^2 \cos(x) dx$
6. $\int \dfrac{(\sin(x))^2}{\cos(x)} dx$

Check your solutions.

1. Let $u = \cos(x)$, and $du = -\sin(x) dx$. Then this integral becomes $\int -\ln|u| du$. The rest of this requires more work to figure out.
2. This is not solvable using $u$-$du$ substitution.
3. This is not solvable using $u$-$du$ substitution.
4. Let $u = x^2, du= 2x dx$. This integral becomes $\frac{1}{2} \int \sin(u) du$.
5. Let $u = \sin(x), du = \cos(x) dx$. This integral becomes $\int u^2 du$.
6. This integral is not solvable using $u$-$du$ substitution.

Computing Definite Integrals

Method 1: Convert back to $x$

Let’s use this technique to help compute $\int\limits_0^2 x^2 \sqrt{x^3 + 1} dx$. Let $u = x^3 + 1$, and $du = 3x^2 dx$. There are two ways to proceed here, and either method is valid. The first method:

• Turn this into an indefinite integral: $\frac{1}{3} \int \sqrt{u} du$.
• Integrate: $\frac{1}{3} \int u^{1/2} du = \frac{2}{9} u^{3/2}$. (We can ignore the constant since we will be doing a definite integral).
  • We cannot plug in here! We now have an antiderivative in terms of $u$, and our bounds are in terms of $x$. So we first need to convert our antiderivative to be in terms of $x$.
• Turn this back into $x$’s: $\frac{2}{9} (x^3 + 1)^{3/2}$
• Then plug in the upper and lower bounds:
  • $x = 2$: $\frac{2}{9}(2^3 + 1)^{3/2} = \frac{2}{9} (\sqrt{9})^3 = \frac{54}{9}$
  • $x = 0$: $\frac{2}{9}(0^3 + 1)^{3/2} = \frac{2}{9}$
  • Subtract: $\frac{54}{9} - \frac{2}{9} = \frac{52}{9}$

This method works fine, and is fairly simple to use. Just be sure not to forget about the upper and lower bounds at the end. To remind myself, I often keep in the bounds, but identify them as bounds in terms of $x$, and not $u$. For example: $\frac{1}{3}\int\limits_{x=0}^{x=2} \sqrt{u} du$, so that I know not to plug in the $x$ values into the $u$ variable.

Method 2: Update the bounds / keep $u$

This next method works just as well: here we change the bounds of integration to be in terms of the $u$ variable. Let’s look at the following problem:

\[\int_{\pi/4}^{\pi/2} \frac{\cos(x)}{(\sin(x))^2} dx\]

Let $u = \sin(x)$, and $du = \cos(x) dx$. Then update the bounds:

• $x = \pi/4$ means $u = \sin(\pi/4) = \sqrt{2}/2$
• $x = \pi/2$ means $u = \sin(\pi/2) = 1$

So now our integral looks like:

\[\int_{\sqrt{2}/2}^1 \frac{1}{u^2} du\]

Use the reverse power rule here and we get $\left.-u^{-1}\right|_{\sqrt{2}/2}^1$, which is $-1 + \sqrt{2}$, or $\sqrt{2} - 1$. Notice, for this method, we never switch back to $x$!

Either method is fine. Sometimes, one method works better than the other, and so it’s good to have both methods at your disposal. Just be sure not to mix them up: don’t update the bounds and then also convert everything back to $x$.

To practice these methods, please take a look at exercises 292-297 and 306-312 in Section 5.5 of the textbook.