Calculus I Lesson 19: Antiderivatives and Introduction to Integrals

1. Warm Up
   1. Questions?
2. Antiderivatives
   1. Reverse Power Rule
   2. Sine and Cosine
   3. $e^x$ and $\ln(x)$
3. Practice Problems
4. Preview: Areas under Curves
5. Reminders

Warm Up

Use l’Hopital’s rule to compute the following limits:

1. $\lim\limits_{x \rightarrow 3} \dfrac{2\tan(6 - 2x)}{3e^{x - 3} - 3}$. (Recall: the derivative of $\tan(x)$ is $\sec^2(x)$.)
2. $\lim\limits_{x \rightarrow \infty} x e^{1 / x}$. (Hint: write this as a fraction).

Questions?

• DeltaMath HW due tonight?
• Written HW due Monday?
• Exam 2 questions?

Antiderivatives

As we’ve mentioned earlier in the semester, the two main topics in calculus are rates of change (derivatives), and areas under curves (integrals). We are almost ready to start studying areas under curves: we’ll be considering this later on in the week. To some degree, these are inverse operations of each other. But before we cover areas under curves, we will need to actually look at “antiderivatives”. Given a function $f(x)$ an antiderivative is a function $F(x)$ such that $F^\prime(x) = f(x)$.

Example: Find an antiderivative of $f(x) = 1$.

• $F(x) = x$ is an antiderivative of $f(x)$, since $F^\prime(x) = 1$.
• $G(x) = x + 1$ is also an antiderivative of $f(x)$, since $G^\prime(x) = 1$ also!

In general, functions do not have just one antiderivative. As we’ve seen, $f^\prime(x) = g^\prime(x)$ means that $f$ and $g$ differ by a constant. That means all antiderivatives of the same function also differ by a constant.

We write this using “indefinite integral” notation: $\int f(x) dx = F(x) + C$, if $F(x)$ is an antiderivative of $f(x)$. We will explore a few examples of functions and see if we can spot some patterns for antiderivatives. In general, we just need to find one antiderivative, and all others differ from that by some constant.

Reverse Power Rule

Exercise: Find the derivatives of the following:

1. $x^2$
2. $x^3$.
3. $x^4$.

From this, we can tell that an antiderivative of $2x$ is $x^2$, an antiderivative of $3x^2$ is $x^3$, and an antiderivative of $4x^3$ is $x^4$.

But what would an antiderivative of $x$ be? It can’t be $x^2$, since the derivative of $x^2$ is $2x$. So it has to be half of that! Notice that $(\frac{x^2}{2})^\prime = \frac{2x}{2} = x$! That is: $\int x dx = \frac{x^2}{2} + C$, where $C$ is any constant.

What’s an antiderivative of $x^2$ then? If $(x^3)^\prime = 3x^2$, we need one-third of this: so $\int x^2 dx = \frac{x^3}{3} + C$. Do you see a pattern?

In general: $(x^n)^\prime = n x^{n-1}$ is our power rule for derivatives. Subtract one from the power, and multiply by the old power.

For antiderivatives, can you figure out the pattern? $\int x^2 dx = \frac{x^3}{3} + C$, $\int x^3 dx = \frac{x^4}{4} + C$, etc. How can you describe the pattern?

Exercise: Using the “reverse” power rule (for antiderivatives), find antiderivatives of the following:

1. $x^2 - 2x + 1$
2. $3x^3 + 3x^2 + 6x + 10$
3. $24x^3 - 6x^2 + 8x - 15$
4. $2\sqrt{x} - \frac{1}{x^2}$.

Check your answers

1. $\frac{x^3}{3} - x^2 + x + C$
2. $\frac{3x^4}{4} + x^3 + 3x^2 + 10x + C$
3. $6x^4 - 2x^3 + 4x^2 - 15x + C$
4. $\frac{2}{3} x^{3/2} + \frac{1}{x}$. Notice that writing everything in exponent form will help, and then you just use the same rule: increase the power by one, and then divide by the new power.

Sine and Cosine

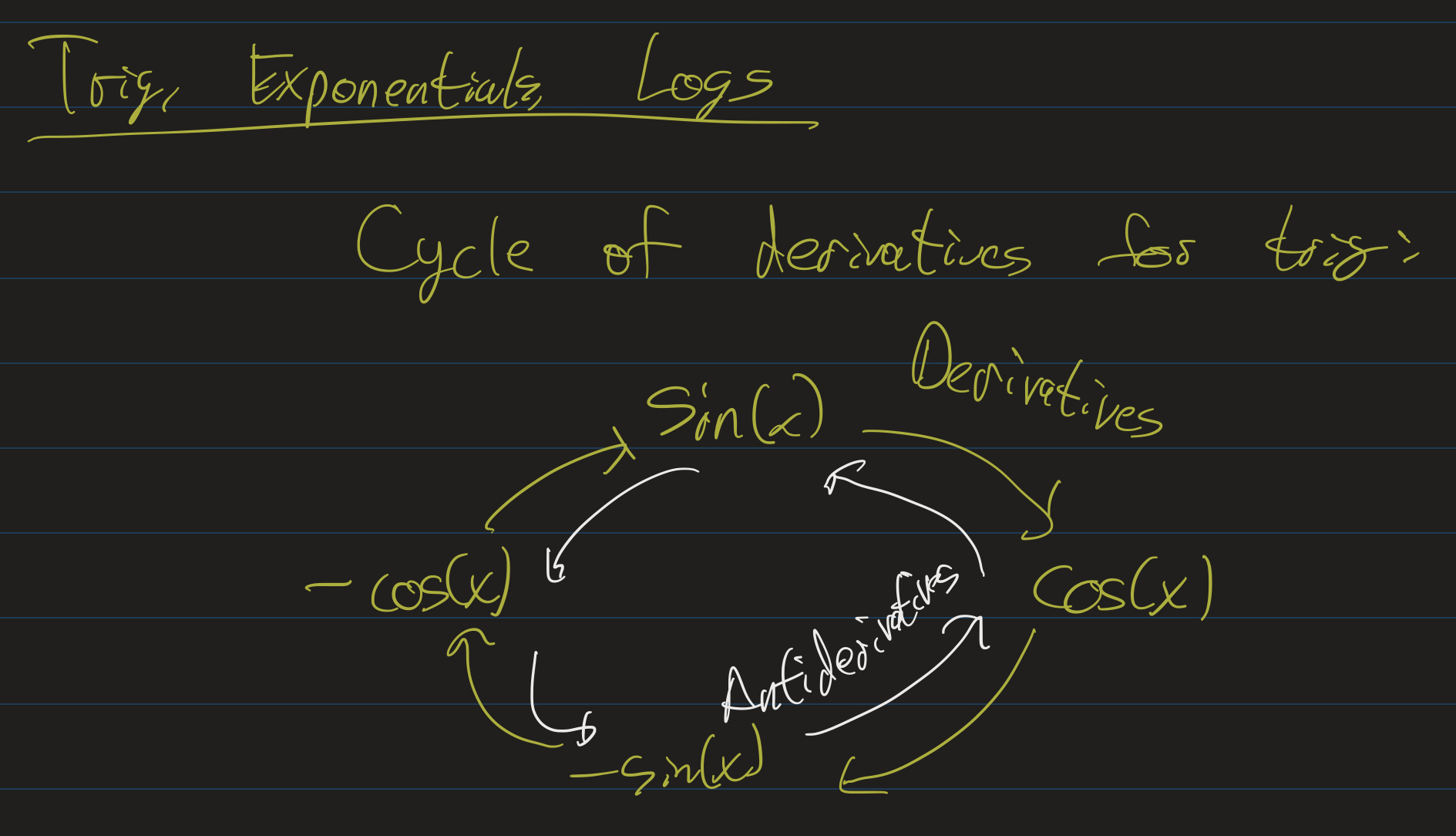
If we remember our trig derivatives, antiderivatives are not much harder:

• $(\sin(x))^\prime = \cos(x)$, so $\int \cos(x) dx = \sin(x) + C$
• $(\cos(x))^\prime = -\sin(x)$, so $\int -\sin(x) dx = \cos(x) + C$.
• Negating this last one, we get $\int \sin(x) dx = -\cos(x) + C$.

Recall that we had a cyclical picture of the derivatives of $\sin(x)$, $\cos(x)$, $-\sin(x)$ and $-\cos(x)$. This is the same pattern for antiderivatives, but in reverse!

$e^x$ and $\ln(x)$

Similarly, if we remember derivative of $e^x$ and $\ln(x)$ we can use them to figure out antiderivatives:

• $(e^x)^\prime = e^x$, so $\int e^x dx = e^x + C$
• $(\ln(x))^\prime = \frac{1}{x}$, so $\int \frac{1}{x} dx = \ln(x) + C$.

Notice this last one seems to mess up our “reverse power rule”. Why can’t we think of $\frac{1}{x}$ as $x^{-1}$ and use the “increase power by one, divide by the new power” rule? (What happens when you try that for $x^{-1}$?)

What about $e^{2x}$? Can you figure out what an antiderivative of $e^{2x}$ is? Notice that since $(e^{2x})^\prime = 2e^{2x}$, then our antiderivative must be half of that, $\frac{e^{2x}}{2}$. Similarly, the an antiderivative of $\cos(2x)$ is $\frac{\sin(2x)}{2}$.

Practice Problems

I hope that you understand the main ideas here, but please make sure to practice this skill as much as possible. Take a look at Section 4.10, exercises 465-467, 470-473, and 496-498. In addition, there is a DeltaMath assignment on this topic due next Thursday 11/20.

Preview: Areas under Curves

As we’ve mentioned earlier in the semester, the two main topics in calculus are rates of change (derivatives), and areas under curves (integrals). We are ready to start studying areas under curves: we’ll be considering this later on in the week. For now, take a look at this video from 3Blue1Brown, which gives us some intuition of why there is a connection between these two topics and, in particular, why integrals are a kind of “inverse” operation to derivatives. This is why we study antiderivatives before we study areas under curves!

Reminders

1. DeltaMath HW 10 due tonight.
2. Written HW 7 due Monday.
3. DeltaMath HW 11 due next Thursday (11/20)
4. Final Paper Rough Draft due on 11/24.
5. Guest Lectures
   • Tomorrow, 11/14: Ted Gulesserian on applications of AI. (10:30 in NS 3052)
   • Nov 24: Ricard Pravia (Morgan Stanley) on careers in finance technology (12:30 PM, here)